
 如图,在△ABC中,AB=AC=2$\sqrt{3}$,∠BAC=120°,点D、E都在边BC上,∠DAE=60°.若BD=2CE,则DE的长为3$\sqrt{3}$-3.
如图,在△ABC中,AB=AC=2$\sqrt{3}$,∠BAC=120°,点D、E都在边BC上,∠DAE=60°.若BD=2CE,则DE的长为3$\sqrt{3}$-3. 分析 (方法一)将△ABD绕点A逆时针旋转120°得到△ACF,连接EF,过点E作EM⊥CF于点M,过点A作AN⊥BC于点N,由AB=AC=2$\sqrt{3}$、∠BAC=120°,可得出BC=6、∠B=∠ACB=30°,通过角的计算可得出∠FAE=60°,结合旋转的性质可证出△ADE≌△AFE(SAS),进而可得出DE=FE,设CE=2x,则CM=x,EM=$\sqrt{3}$x、FM=4x-x=3x、EF=ED=6-6x,在Rt△EFM中利用勾股定理可得出关于x的一元二次方程,解之可得出x的值,再将其代入DE=6-6x中即可求出DE的长.
(方法二)将△ABD绕点A逆时针旋转120°得到△ACF,取CF的中点G,连接EF、EG,由AB=AC=2$\sqrt{3}$、∠BAC=120°,可得出∠ACB=∠B=30°,根据旋转的性质可得出∠ECG=60°,结合CF=BD=2CE可得出△CEG为等边三角形,进而得出△CEF为直角三角形,通过解直角三角形求出BC的长度以及证明全等找出DE=FE,设EC=x,则BD=CD=2x,DE=FE=6-3x,在Rt△CEF中利用勾股定理可得出FE=$\sqrt{3}$x,利用FE=6-3x=$\sqrt{3}$x可求出x以及FE的值,此题得解.
解答 解:(方法一)将△ABD绕点A逆时针旋转120°得到△ACF,连接EF,过点E作EM⊥CF于点M,过点A作AN⊥BC于点N,如图所示.
∵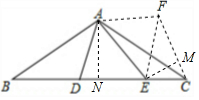 AB=AC=2$\sqrt{3}$,∠BAC=120°,
AB=AC=2$\sqrt{3}$,∠BAC=120°,
∴BN=CN,∠B=∠ACB=30°.
在Rt△BAN中,∠B=30°,AB=2$\sqrt{3}$,
∴AN=$\frac{1}{2}$AB=$\sqrt{3}$,BN=$\sqrt{A{B}^{2}-A{N}^{2}}$=3,
∴BC=6.
∵∠BAC=120°,∠DAE=60°,
∴∠BAD+∠CAE=60°,
∴∠FAE=∠FAC+∠CAE=∠BAD+∠CAE=60°.
在△ADE和△AFE中,$\left\{\begin{array}{l}{AD=AF}\\{∠DAE=∠FAE=60°}\\{AE=AE}\end{array}\right.$,
∴△ADE≌△AFE(SAS),
∴DE=FE.
∵BD=2CE,BD=CF,∠ACF=∠B=30°,
∴设CE=2x,则CM=x,EM=$\sqrt{3}$x,FM=4x-x=3x,EF=ED=6-6x.
在Rt△EFM中,FE=6-6x,FM=3x,EM=$\sqrt{3}$x,
∴EF2=FM2+EM2,即(6-6x)2=(3x)2+($\sqrt{3}$x)2,
解得:x1=$\frac{3-\sqrt{3}}{2}$,x2=$\frac{3+\sqrt{3}}{2}$(不合题意,舍去),
∴DE=6-6x=3$\sqrt{3}$-3.
故答案为:3$\sqrt{3}$-3.
(方法二):将△ABD绕点A逆时针旋转120°得到△ACF,取CF的中点G,连接EF、EG,如图所示.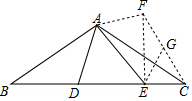
∵AB=AC=2$\sqrt{3}$,∠BAC=120°,
∴∠ACB=∠B=∠ACF=30°,
∴∠ECG=60°.
∵CF=BD=2CE,
∴CG=CE,
∴△CEG为等边三角形,
∴EG=CG=FG,
∴∠EFG=∠FEG=$\frac{1}{2}$∠CGE=30°,
∴△CEF为直角三角形.
∵∠BAC=120°,∠DAE=60°,
∴∠BAD+∠CAE=60°,
∴∠FAE=∠FAC+∠CAE=∠BAD+∠CAE=60°.
在△ADE和△AFE中,$\left\{\begin{array}{l}{AD=AF}\\{∠DAE=∠FAE=60°}\\{AE=AE}\end{array}\right.$,
∴△ADE≌△AFE(SAS),
∴DE=FE.
设EC=x,则BD=CD=2x,DE=FE=6-3x,
在Rt△CEF中,∠CEF=90°,CF=2x,EC=x,
EF=$\sqrt{C{F}^{2}-E{C}^{2}}$=$\sqrt{3}$x,
∴6-3x=$\sqrt{3}$x,
x=3-$\sqrt{3}$,
∴DE=$\sqrt{3}$x=3$\sqrt{3}$-3.
故答案为:3$\sqrt{3}$-3.
点评 本题考查了全等三角形的判定与性质、勾股定理、解一元二次方程以及旋转的性质,通过勾股定理找出关于x的一元二次方程是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
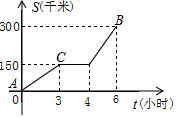 司机小王开车从A地出发去B地送信,其行驶路程与时间函数关系图象如图所示,当汽车行驶若干小时到达C地时,汽车发生了故障,需停车检修,修理了一段时间后,为了按时赶到B地,汽车加快了速度,结果正好按时赶到,根据题意及图回答下列问题:
司机小王开车从A地出发去B地送信,其行驶路程与时间函数关系图象如图所示,当汽车行驶若干小时到达C地时,汽车发生了故障,需停车检修,修理了一段时间后,为了按时赶到B地,汽车加快了速度,结果正好按时赶到,根据题意及图回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | AD∥BC | B. | AD=BC | C. | AB∥CD | D. | OB=OD |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com