

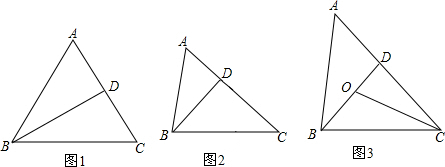
分析 (1)先证明BD=DC,再证明EM、MF分别是△ABD,△ADC的中位线即可.
(2)结论:MN∥AC,只要证明$\frac{EM}{MF}$=$\frac{EN}{NC}$即可.
(3)如图3中,作DN∥AB交CE于N,CM⊥AD交AD的延长线于M,不妨设AE=a.则AB=3a,EB=2a.BC=2$\sqrt{3}$a,BD=DC=$\sqrt{3}$a,由tan∠BAD═$\frac{BD}{AB}$=$\frac{\sqrt{3}}{3}$,推出∠BAD=30°,∠DCM=30°,再证明△AEQ≌△DNQ,得AQ=QD,求出QD即可解决问题.
解答 (1)证明:如图1中,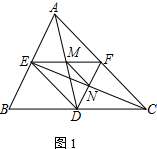
∵AE=EB,EF∥AC,
∴AF=FC,AM=MD,∵FD∥AB,
∴BD=CD,
∴EM=$\frac{1}{2}$BD,MF=$\frac{1}{2}$CD,
∴EM=MF.
(2)结论:MN∥AC.
证明:如图2中,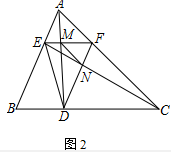
∵AE∥DF,
∴$\frac{EM}{MF}$=$\frac{AM}{DM}$,
∵MF∥BC,
∴$\frac{AM}{DM}$=$\frac{AF}{FC}$,
∵FN∥AE,
∴$\frac{AF}{FC}$=$\frac{EN}{NC}$,
∴$\frac{EM}{MF}$=$\frac{EN}{NC}$,
∴MN∥CF.
(3)如图3中,作DN∥AB交CE于N,CM⊥AD交AD的延长线于M.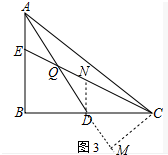
∵AE:AB:BC=1:3:2$\sqrt{3}$,
不妨设AE=a.则AB=3a,EB=2a.BC=2$\sqrt{3}$a,BD=DC=$\sqrt{3}$a,
∴tan∠BAD═$\frac{BD}{AB}$=$\frac{\sqrt{3}}{3}$,
∴∠BAD=30°,∠ADB=∠CDM=60°,
∴∠DCM=30°,
∴DM=$\frac{\sqrt{3}}{2}$a,CM=$\frac{3}{2}$a,'
∵BD=DC,DN∥EB,
∴EN=NC,
∴DN=$\frac{1}{2}$EB=a=AE,
∵AE∥DN,
∴∠EAQ=∠NDQ,
在△AEQ和△DNQ中,
$\left\{\begin{array}{l}{∠EAQ=∠QDN}\\{∠EQA=∠DQN}\\{AE=DN}\end{array}\right.$,
∴△AEQ≌△DNQ,
∴AQ=QD,
∵AD=$\sqrt{A{B}^{2}+B{D}^{2}}$=$\sqrt{(3a)^{2}+(\sqrt{3}a)^{2}}$=2$\sqrt{3}$a,
∴DQ=$\sqrt{3}$a,QM=DQ+DM=$\frac{3\sqrt{3}}{2}$a,
∴tan∠CQD=$\frac{CM}{QM}$=$\frac{\frac{3}{2}a}{\frac{3\sqrt{3}}{2}a}$=$\frac{\sqrt{3}}{3}$.
点评 本题考查三角形综合题、平行线分线段成比例定理、三角形的中位线定理、全等三角形的判定和性质、勾股定理、平行线的判定等知识,解题的关键是学会利用比例式证明两条直线平行,学会添加常用辅助线,构造三角形中位线解决问题,属于中考压轴题.


 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:初中数学 来源: 题型:解答题
 如图,扇形OAB的圆心角∠AOB=120°,半径OA=6cm.
如图,扇形OAB的圆心角∠AOB=120°,半径OA=6cm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 9 | B. | -9 | C. | $\frac{1}{9\;}$ | D. | $-\frac{1}{9\;}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
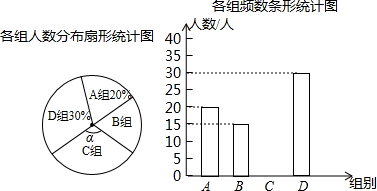 小强同学对本校学生完成家庭作业的时间进行了随机抽样调查,并绘成如下不完整的三个统计图表.
小强同学对本校学生完成家庭作业的时间进行了随机抽样调查,并绘成如下不完整的三个统计图表.| 组别 | 时间(小时) | 频数(人) | 频率 |
| A | 0≤x≤0.5 | 20 | 0.2 |
| B | 0.5<x≤1 | 15 | a |
| C | 1<x≤1.5 | 35 | 0.35 |
| D | x>1.5 | 30 | 0.3 |
| 合计 | b | 1.0 | |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com