
【题目】如图,等腰直角![]() 的顶点
的顶点![]() 在正方形
在正方形![]() 的对角线
的对角线![]() 上,
上,![]() 所在的直线交
所在的直线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() . 下列结论中,正确的有_________ (填序号).
. 下列结论中,正确的有_________ (填序号).
①![]() ;②
;②![]() 是
是![]() 的一个三等分点;③
的一个三等分点;③![]() ;④
;④![]() ;⑤
;⑤![]() .
.

【答案】①②④
【解析】
根据△CBE≌△CDF即可判断①;由△CBE≌△CDF得出∠EBC=∠FDC=45°进而得出△DEF为直角三角形结合![]() 即可判断②;判断△BEN是否相似于△BCE即可判断③;根据△BNE∽△DME即可判断④;作EH⊥BC于点H得出△EHC∽△FDE结合tan∠HEC=tan∠DFE=2,设出线段比即可判断⑤.
即可判断②;判断△BEN是否相似于△BCE即可判断③;根据△BNE∽△DME即可判断④;作EH⊥BC于点H得出△EHC∽△FDE结合tan∠HEC=tan∠DFE=2,设出线段比即可判断⑤.
∵△CEF为等腰直角三角形
∴CE=CF,∠ECF=90°
又ABCD为正方形
∴∠BCD=90°,BC=DC
又∠BCD=∠BCE+∠ECD
∠ECF=∠ECD+∠DCF
∴∠DCF=∠BCE
∴△CBE≌△CDF(SAS)
∴BE=DF,故①正确;
∴∠EBC=∠FDC=45°
故∠EDF=∠EDC+∠FDC=90°
又![]()
∴E是BD的一个三等分点,故②正确;
∵![]()
∴![]()
即判定△BEN∽△BCE
∵△ECF为等腰直角三角形,BD为正方形对角线
∴∠CFE=45°=∠EDC
∴∠CFE+∠MCF=∠EDC+∠DEM
∴∠MCF=∠DEM
然而题目并没有告诉M是EF的中点
∴∠ECM≠∠MCF
∴∠ECM≠∠DEM≠∠BNE
∴不能判定△BEN∽△BCE
∴不能得出![]() 进而不能得出
进而不能得出![]() ,故③错误;
,故③错误;
由题意可知△BNE∽△DME
又BE=2DE
∴BN=2DM,故④正确;
作EH⊥BC于点H
∵∠MCF=∠DEM
又∠HCE=∠DCF
∴∠HCE=∠DEM
又∠EHC=∠FDE=90°
∴△EHC∽△FDE
∴tan∠HEC=tan∠DFE=2
可设EH=x,则CH=2x
EC=![]()
∴sin∠BCE=![]() ,故⑤错误;
,故⑤错误;
故答案为①②④.



科目:初中数学 来源: 题型:
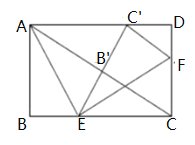
【题目】如图,在矩形ABCD中,AB=4,点E,F分别在BC,CD上,将△ABE沿AE折叠,使点B落在AC上的点B′处,又将△CEF沿EF折叠,使点C落在直线EB′与AD的交点C′处,DF=_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图一座拱桥的示意图,已知桥洞的拱形是抛物线.当水面宽为12m时,桥洞顶部离水面4m.、

(1)建立平面直角坐标系,并求该抛物线的函数表达式;
(2)若水面上升1m,水面宽度将减少多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,过点
,过点![]() 的直线
的直线![]() ,
,![]() 为
为![]() 边上一点,过点
边上一点,过点![]() 作
作![]() ,交直线
,交直线![]() 于
于![]() ,垂足为
,垂足为![]() ,连接
,连接![]() 、
、![]()

(1)当![]() 在
在![]() 中点时,四边形
中点时,四边形![]() 是什么特殊四边形?说明你的理由;
是什么特殊四边形?说明你的理由;
(2)当![]() 为
为![]() 中点时,
中点时,![]() 等于 度时,四边形
等于 度时,四边形![]() 是正方形.
是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
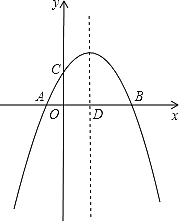
【题目】如图,抛物线![]() 与
与![]() 轴交于A、B两点,与
轴交于A、B两点,与![]() 轴交于点C,抛物线的对称轴交
轴交于点C,抛物线的对称轴交![]() 轴于点D,已知点A的坐标为(-1,0),点C的坐标为(0,2).
轴于点D,已知点A的坐标为(-1,0),点C的坐标为(0,2).
(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() (
(![]() 是常数)经过点
是常数)经过点![]() .
.
(1)求该抛物线的解析式和顶点坐标.
(2)若点![]() 在抛物线上,且点
在抛物线上,且点![]() 关于原点的对称点为
关于原点的对称点为![]() .
.
①当点![]() 落在该抛物线上时,求
落在该抛物线上时,求![]() 的值;
的值;
②当点![]() 落在第二象限内,
落在第二象限内,![]() 取得最小值时,求
取得最小值时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
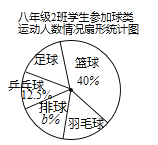
【题目】某校要求八年级同学在课外活动中,必须在五项球类(篮球、足球、排球、羽毛球、乒乓球)活动中任选一项(只能选一项)参加训练,为了了解八年级学生参加球类活动的整体情况,现以八年级2班作为样本,对该班学生参加球类活动的情况进行统计,并绘制了如图所示的不完整统计表和扇形统计图:

根据图中提供的信息,解答下列问题:
(1)a= ,b= ;
(2)该校八年级学生共有600人,则该年级参加足球活动的人数约 人;
(3)该班参加乒乓球活动的5位同学中,有3位男同学(A,B,C)和2位女同学(D,E),现准备从中选取两名同学组成双打组合,用树状图或列表法求恰好选出一男一女组成混合双打组合的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重庆八中某数学兴趣小组同学探究函数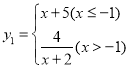 的图象与性质,根据学习函数的经验,该小组进行了系列探究.
的图象与性质,根据学习函数的经验,该小组进行了系列探究.
下表给出了自变量![]() 与函数
与函数![]() 的一些对应值:
的一些对应值:
| … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | … |
| … | 2 | 3 | 4 |
|
| 1 |
| … |
(1)补全表格:![]() ,
,![]() ;
;
(2)在如图所示的面直角坐标系中,补全函数的图象并写出该函数的一条性质:
____________________________________________________________________________;
(3)若函数![]() ,直接写出不等式
,直接写出不等式![]() 的解集.
的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】B,C是⊙O上的两个定点,A是圆上的动点,0°<∠BAC<90°,BD∥AC,CD∥AB.
(1)如图1,如果△ABC是等边三角形,求证BD是⊙O的切线:
(2)如图2,如果60°<∠BAC<90°,BD,CD分别交⊙O于E,F,研究五边形ABEFC的性质;
①探索AE、AF和BC的数量关系,并证明你的结论:
②如图3,若⊙O的半径为4,∠BAC=75°,求边EF的长;
③若AB=c,AC=b,直接写出BE,CF的数量关系.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com