
【题目】如图,直线y=﹣ ![]() x+2
x+2 ![]() 与x轴,y轴分别交于点A,点B,两动点D,E分别从点A,点B同时出发向点O运动(运动到点O停止),运动速度分别是1个单位长度/秒和
与x轴,y轴分别交于点A,点B,两动点D,E分别从点A,点B同时出发向点O运动(运动到点O停止),运动速度分别是1个单位长度/秒和 ![]() 个单位长度/秒,设运动时间为t秒,以点A为顶点的抛物线经过点E,过点E作x轴的平行线,与抛物线的另一个交点为点G,与AB相交于点F.
个单位长度/秒,设运动时间为t秒,以点A为顶点的抛物线经过点E,过点E作x轴的平行线,与抛物线的另一个交点为点G,与AB相交于点F.
(1)求点A,点B的坐标;
(2)用含t的代数式分别表示EF和AF的长;
(3)当四边形ADEF为菱形时,试判断△AFG与△AGB是否相似,并说明理由.
(4)是否存在t的值,使△AGF为直角三角形?若存在,求出这时抛物线的解析式;若不存在,请说明理由.
【答案】
(1)解:在直线y=﹣ ![]() x+2
x+2 ![]() 中,
中,
令y=0可得0=﹣ ![]() x+2
x+2 ![]() ,解得x=2,
,解得x=2,
令x=0可得y=2 ![]() ,
,
∴A为(2,0),B为(0,2 ![]() );
);
(2)解:由(1)可知OA=2,OB=2 ![]() ,
,
∴tan∠ABO= ![]() =
= ![]() ,
,
∴∠ABO=30°,
∵运动时间为t秒,
∴BE= ![]() t,
t,
∵EF∥x轴,
∴在Rt△BEF中,EF=BEtan∠ABO= ![]() BE=t,BF=2EF=2t,
BE=t,BF=2EF=2t,
在Rt△ABO中,OA=2,OB=2 ![]() ,
,
∴AB=4,
∴AF=4﹣2t;
(3)解:相似.理由如下:
当四边形ADEF为菱形时,则有EF=AF,
即t=4﹣2t,解得t= ![]() ,
,
∴AF=4﹣2t=4﹣ ![]() =
= ![]() ,OE=OB﹣BE=2
,OE=OB﹣BE=2 ![]() ﹣
﹣ ![]() ×
× ![]() =
= ![]() ,
,
如图,过G作GH⊥x轴,交x轴于点H,
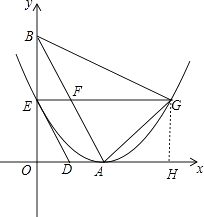
则四边形OEGH为矩形,
∴GH=OE= ![]() ,
,
又EG∥x轴,抛物线的顶点为A,
∴OA=AH=2,
在Rt△AGH中,由勾股定理可得AG2=GH2+AH2=( ![]() )2+22=
)2+22= ![]() ,
,
又AFAB= ![]() ×4=
×4= ![]() ,
,
∴AFAB=AG2,即 ![]() =
= ![]() ,且∠FAG=∠GAB,
,且∠FAG=∠GAB,
∴△AFG∽△AGB;
(4)解:存在,
∵EG∥x轴,
∴∠GFA=∠BAO=60°,
又G点不能在抛物线的对称轴上,
∴∠FGA≠90°,
∴当△AGF为直角三角形时,则有∠FAG=90°,
又∠FGA=30°,
∴FG=2AF,
∵EF=t,EG=4,
∴FG=4﹣t,且AF=4﹣2t,
∴4﹣t=2(4﹣2t),
解得t= ![]() ,
,
即当t的值为 ![]() 秒时,△AGF为直角三角形,此时OE=OB﹣BE=2
秒时,△AGF为直角三角形,此时OE=OB﹣BE=2 ![]() ﹣
﹣ ![]() t=2
t=2 ![]() ﹣
﹣ ![]() ×
× ![]() =
= ![]() ,
,
∴E点坐标为(0, ![]() ),
),
∵抛物线的顶点为A,
∴可设抛物线解析式为y=a(x﹣2)2,
把E点坐标代入可得 ![]() =4a,解得a=
=4a,解得a= ![]() ,
,
∴抛物线解析式为y= ![]() (x﹣2)2,
(x﹣2)2,
即y= ![]() x2﹣
x2﹣ ![]() x+
x+ ![]() .
.
【解析】(1)在直线y=﹣ 3 x+23 中,令y=0,x=0,得到A为(2,0),B为(0,2 ![]() );(2)由(1)可知OA=2,OB=2 3 ,得到tan∠ABO
);(2)由(1)可知OA=2,OB=2 3 ,得到tan∠ABO![]()
![]() ,由∠ABO=30°,由运动时间为t秒,得到BE=
,由∠ABO=30°,由运动时间为t秒,得到BE= ![]() t,EF∥x轴,所以在Rt△BEF中,EF=BEtan∠ABO=t,BF=2EF=2t,在Rt△ABO中,OA=2,OB=2
t,EF∥x轴,所以在Rt△BEF中,EF=BEtan∠ABO=t,BF=2EF=2t,在Rt△ABO中,OA=2,OB=2 ![]() ,所以AB=4,AF=4﹣2t;(3)当四边形ADEF为菱形时,则有EF=AF,即t=4﹣2t,得到AF=4﹣2t=
,所以AB=4,AF=4﹣2t;(3)当四边形ADEF为菱形时,则有EF=AF,即t=4﹣2t,得到AF=4﹣2t= ![]() ,OE=OB﹣BE=
,OE=OB﹣BE= ![]() ,由图知四边形OEGH为矩形,得到GH=OE,又EG∥x轴,抛物线的顶点为A,得到OA=AH=2,在Rt△AGH中,由勾股定理可得AG2=GH2+AH2 ,得到AFAB=AG2,且∠FAG=∠GAB,得到△AFG∽△AGB;(4)由EG∥x轴,得到∠GFA=∠BAO=60°,又G点不能在抛物线的对称轴上,所以∠FGA≠90°,当△AGF为直角三角形时,则有∠FAG=90°,又∠FGA=30°,得到FG=2AF,由EF=t,EG=4,得到FG=4﹣t,且AF=4﹣2t,即当t的值为
,由图知四边形OEGH为矩形,得到GH=OE,又EG∥x轴,抛物线的顶点为A,得到OA=AH=2,在Rt△AGH中,由勾股定理可得AG2=GH2+AH2 ,得到AFAB=AG2,且∠FAG=∠GAB,得到△AFG∽△AGB;(4)由EG∥x轴,得到∠GFA=∠BAO=60°,又G点不能在抛物线的对称轴上,所以∠FGA≠90°,当△AGF为直角三角形时,则有∠FAG=90°,又∠FGA=30°,得到FG=2AF,由EF=t,EG=4,得到FG=4﹣t,且AF=4﹣2t,即当t的值为 ![]() 秒时,△AGF为直角三角形,此时OE=OB﹣BE,即E点坐标为(0,
秒时,△AGF为直角三角形,此时OE=OB﹣BE,即E点坐标为(0, ![]() ),由抛物线的顶点为A,得到可设抛物线解析式为y=a(x﹣2)2,把E点坐标代入可得
),由抛物线的顶点为A,得到可设抛物线解析式为y=a(x﹣2)2,把E点坐标代入可得 ![]() =4a,解得a=
=4a,解得a= ![]() ,所以抛物线解析式为y=
,所以抛物线解析式为y= ![]() (x﹣2)2,即y=
(x﹣2)2,即y= ![]() x2﹣
x2﹣ ![]() x+
x+ ![]() .
.
【考点精析】利用相似三角形的判定对题目进行判断即可得到答案,需要熟知相似三角形的判定方法:两角对应相等,两三角形相似(ASA);直角三角形被斜边上的高分成的两个直角三角形和原三角形相似; 两边对应成比例且夹角相等,两三角形相似(SAS);三边对应成比例,两三角形相似(SSS).


科目:初中数学 来源: 题型:
【题目】如图,贵阳市某中学数学活动小组在学习了“利用三角函数测高”后.选定测量小河对岸一幢建筑物BC的高度.他们先在斜坡上的D处,测得建筑物顶的仰角为30°.且D离地面的高度DE=5m.坡底EA=10m,然后在A处测得建筑物顶B的仰角是50°,点E,A,C在同一水平线上,求建筑物BC的高.(结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四张编号为A,B,C,D的卡片(除编号外,其余完全相同)的正面分别写上如图所示的正整数后,背面向上,洗匀放好.
(1)我们知道,满足a2+b2=c2的三个正整数a,b,c成为勾股数,嘉嘉从中随机抽取一张,求抽到的卡片上的数是勾股数的概率P1;
(2)琪琪从中随机抽取一张(不放回),再从剩下的卡片中随机抽取一张(卡片用A,B,C,D表示).请用列表或画树形图的方法求抽到的两张卡片上的数都是勾股数的概率P2 , 并指出她与嘉嘉抽到勾股数的可能性一样吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】y= ![]() x+1是关于x的一次函数,则一元二次方程kx2+2x+1=0的根的情况为( )
x+1是关于x的一次函数,则一元二次方程kx2+2x+1=0的根的情况为( )
A.没有实数根
B.有一个实数根
C.有两个不相等的实数根
D.有两个相等的实数根
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,过点A(﹣ ![]() ,0)的两条直线分别交y轴于B,C两点,且B,C两点的纵坐标分别是一元二次方程x2﹣2x﹣3=0的两个根.
,0)的两条直线分别交y轴于B,C两点,且B,C两点的纵坐标分别是一元二次方程x2﹣2x﹣3=0的两个根.
(1)求线段BC的长度;
(2)试问:直线AC与直线AB是否垂直?请说明理由;
(3)若点D在直线AC上,且DB=DC,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果两个角之差的绝对值等于60°,则称这两个角互为“互优角”,(本题中所有角都是指大于0°且小于180°的角).
(1)若∠1和∠2互为“互优角”,当∠1=90°时,则∠2=_____°;
(2)如图1,将一长方形纸片沿着EP对折(点P在线段BC上,点E在线段AB上)使点B落在点若与互为“互优角”,求∠BPE的度数;
(3)再将纸片沿着PF对折(点F在线段CD或AD上)使点C落在C′:
①如图2,若点E、C′、P在同一直线上,且![]() 与
与![]() 互为“互优角”,求∠EPF的度数(对折时,线段落在∠EPF内部);
互为“互优角”,求∠EPF的度数(对折时,线段落在∠EPF内部);
②若∠B′PC′与∠EPF互为“互优角”,则∠BPE求∠CPF应满足什么样的数量关系(直接写出结果即可).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣4与x轴交于A(4,0)、B(﹣2,0)两点,与y轴交于点C,点P是线段AB上一动点(端点除外),过点P作PD∥AC,交BC于点D,连接CP.
(1)求该抛物线的解析式;
(2)当动点P运动到何处时,BP2=BDBC;
(3)当△PCD的面积最大时,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com