
【题目】如图,点E为正方形ABCD的边BC所在直线上的一点,连接AE,过点C作CF⊥AE于F,连接BF.

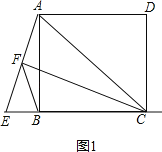
(1)如图1,当点E在CB的延长线上,且AC=EC时,求证:BF=![]() ;
;
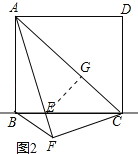
(2)如图2,当点E在线段BC上,且AE平分∠BAC时,求证:AB+BE=AC;
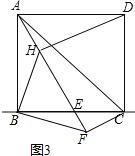
(3)如图3,当点E继续往右运动到BC中点时,过点D作DH⊥AE于H,连接BH.求证:∠BHF=45°.
【答案】见解析
【解析】
试题分析:(1)根据等腰三角形的性质和直角三角形斜边中线的性质即可证得结论;
(2)作EG⊥AC于G,根据角平分线的性质得出BE=EG,进而通过RT△ABE≌RT△AGE得出AG=AB,然后证得△EGC是等腰直角三角形,从而证得EG=GC,即可证得AB+BE=AC;
(3)设正方形的边长为1,则AB=AD=1,BE=EC=![]() ,根据勾股定理求得AE=
,根据勾股定理求得AE=![]() ,然后通过证得△AEB∽△CEF,△ADH∽△EAB,对应边成比例证得CF=AH=
,然后通过证得△AEB∽△CEF,△ADH∽△EAB,对应边成比例证得CF=AH=![]() ,然后根据SAS证得△ABH≌△CBF,证得BH=BF,∠ABH=∠CBF,从而证得△HBF是等腰直角三角形,从而证得∠BHF=45°.
,然后根据SAS证得△ABH≌△CBF,证得BH=BF,∠ABH=∠CBF,从而证得△HBF是等腰直角三角形,从而证得∠BHF=45°.
(1)证明:如图1,∵AC=EC,CF⊥AE,
∴AF=EF,
∴BF是RT△ABE的斜边的中线,
∴BF=![]() AE;
AE;
(2)如图2,作EG⊥AC于G,
∵AE平分∠BAC,AB⊥BE,
∴BE=EG,
在RT△ABE和RT△AGE中
![]() ,
,
∴RT△ABE≌RT△AGE(HL),
∴AG=AB,
∵四边形ABCD是正方形,
∴∠ACB=45°,
∴∠GEC=45°,
∴∠GEC=∠ACB=45°,
∴EG=GC,
∴AB+BE=AG+GC,
即AB+BE=AC;
(3)如图3,设正方形的边长为1,则AB=AD=1,
∵点E是BC中点,
∴BE=EC=![]() ,
,
∴AE=![]() =
=![]() ,
,
∵∠ABE=∠CFE=90°,∠AEB=∠CEF,
∴△AEB∽△CEF,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴CF=![]() ,
,
∵AD∥BC,
∴∠DAH=∠AEB,
∵∠AHD=∠BEA=90°,
∴△ADH∽△EAB,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴AH=![]() ,
,
∴CF=AH,
在△ABH和△CBF中
∴△ABH≌△CBF(SAS),
∴BH=BF,∠ABH=∠CBF,
∵∠ABH+∠HBE=∠ABE=90°,
∴∠HBF=90°,
∴△HBF是等腰直角三角形,
∴∠BHF=45°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】计算:
(1)|-1|+(—2)3+(7-π)0-(![]() )-1;
)-1;
(2) (-2a)3·(a2)2÷a3
(3) (3a+b-2)(3a-b+2)
(4)10002-1002×998
(5) (x+1)(x2+1)(x4+1)(x-1)
(6) (3a+2)2(3a-2)2
查看答案和解析>>
科目:初中数学 来源: 题型:
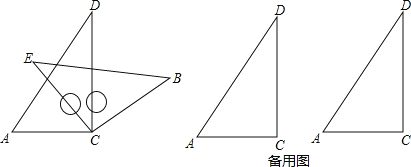
【题目】将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起(其中,∠A=60°,∠D=30°;∠E=∠B=45°):
(1)①若∠DCE=45°,则∠ACB的度数为 ;
②若∠ACB=140°,求∠DCE的度数;
(2)由(1)猜想∠ACB与∠DCE的数量关系,并说明理由.
(3)当∠ACE<180°且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请直接写出∠ACE角度所有可能的值(不必说明理由);若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个二元码是由0和1组成的数字串x1x2…xn(n为正整数),其中xk(k=1,2,…,n)称为第k位码元,如:二元码01101的第1位码元为0,第5位码元为1。
(1)二元码100100的第4位码元为__________;
(2)二元码是通信中常用的码,但在通信过程中有时会发生码元错误(即码元由0变为1,或者由1变为0)。已知某种二元码x1x2…x7的码元满足如下校验方程组:

其中运算![]() 定义为:0
定义为:0![]() 0=0,1
0=0,1![]() 1=0,0
1=0,0![]() 1=1,1
1=1,1![]() 0=1。
0=1。
①计算:0![]() 1
1![]() 1
1![]() 0=___________;
0=___________;
②现已知一个这种二元码在通信过程中仅在第k位发生码元错误后变成了0101101,那么利用上述校验方程组可判定k等于__________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读,然后解答提出的问题:
设a,b是有理数,且满足a+![]() b=3﹣2
b=3﹣2![]() ,求ba的值.
,求ba的值.
解:由题意得(a﹣3)+(b+2)![]() =0,因为a,b都是有理数,所以a﹣3,b+2也是有理数,
=0,因为a,b都是有理数,所以a﹣3,b+2也是有理数,
由于![]() 是无理数,所以a﹣3=0,b+2=0,所以a=3,b=﹣2,所以ba=(﹣2)3=﹣8.问题:设x,y都是有理数,且满足x2﹣2y+
是无理数,所以a﹣3=0,b+2=0,所以a=3,b=﹣2,所以ba=(﹣2)3=﹣8.问题:设x,y都是有理数,且满足x2﹣2y+![]() y=8+4
y=8+4![]() ,求x+y的值.
,求x+y的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在射线OA上,CE平分∠ACD. OF平分∠COB并与射线CD交于点F。
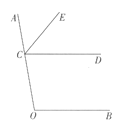
(1)依题意补全图形;
(2)若∠COB+∠OCD=180°,求证:∠ACE=∠COF。
请将下面的证明过程补充完整。
证明:∵CE平分∠ACD,OF平分∠COB,
∴∠ACE=______________,∠COF=![]() ∠COB。
∠COB。
(理由: _____________________________________)
∵点C在射线OA上,
∴∠ACD+∠OCD=180°。
∵∠COB+∠OCD=180°,
∴∠ACD=∠____________。
(理由: ___________________________________)
∴∠ACE=∠COF。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班七个兴趣小组人数分别为4,4,5,x,6,6,7.已知这组数据的平均数是5,则这组数据的中位数是( )
A. 7 B. 6 C. 5 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com