
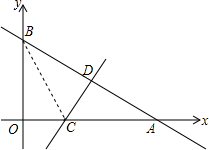
 如图,一次函数y=-$\frac{3}{4}$x+6的图象与x轴和y轴分别交于点A和B,再将△AOB沿直线CD对折,使点A与点B重合.直线CD与x轴交于点C,与AB交于点D.
如图,一次函数y=-$\frac{3}{4}$x+6的图象与x轴和y轴分别交于点A和B,再将△AOB沿直线CD对折,使点A与点B重合.直线CD与x轴交于点C,与AB交于点D.分析 (1)对于一次函数y=-$\frac{3}{4}$x+6,令x=0或y=0,解方程即可解决问题.
(2)设OC=x,则CB=CA=8-x,在Rt△BOC中,根据BC2=OB2+OC2,列出方程即可解决问题.
(3)分两种情形讨论①)①当P在OB上时,OP=$\frac{2}{3}$OB时,三角形OAP的面积等于三角形OAB面积的$\frac{2}{3}$,②当P在AB上时,AP=$\frac{2}{3}$AB时,三角形OAP的面积等于三角形OAB面积的$\frac{2}{3}$,列方程求解即可.
解答 解:(1)对于一次函数y=-$\frac{3}{4}$x+6,令x=0得y=6,令y=0得x=8,
∴A(8,0),B(0,6).
(2)在Rt△AOB中,∵∠AOB=90°,OA=8,OB=6,
∴AB=$\sqrt{O{B}^{2}+O{A}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10,
设OC=x,则CB=CA=8-x,
在Rt△BOC中,∵BC2=OB2+OC2,
∴62+x2=(8-x)2,
∴x=$\frac{7}{4}$,
∴OC=$\frac{7}{4}$.
(3)①当P在OB上时,OP=$\frac{2}{3}$OB时,三角形OAP的面积等于三角形OAB面积的$\frac{2}{3}$,
∴2t=$\frac{2}{3}$×6,
∴t=2,
②当P在AB上时,AP=$\frac{2}{3}$AB时,三角形OAP的面积等于三角形OAB面积的$\frac{2}{3}$,
∴AP=$\frac{20}{3}$,
BP=10-$\frac{20}{3}$=$\frac{10}{3}$,
∴2t=6+$\frac{10}{3}$,
∴t=$\frac{14}{3}$,
综上所述,t=2s或$\frac{14}{3}$s时,三角形OAP的面积等于三角形OAB面积的$\frac{2}{3}$.
点评 本题考查一次函数综合题、三角形的面积公式、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,学会用方程的思想思考问题,属于中考常考题型.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $-\frac{1}{3}$和 0.333 | B. | -[+(-7)]和-(-7) | C. | -24和 (-2)4 | D. | |3-π|和 π-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
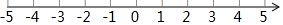 在数轴上表示下列各数,并把这些数按从小到大顺序进行排列,用“<”连接:-1.5,-22,-(-4),0,-|-3|,$\sqrt{9}$.
在数轴上表示下列各数,并把这些数按从小到大顺序进行排列,用“<”连接:-1.5,-22,-(-4),0,-|-3|,$\sqrt{9}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,经过点B(-4,0)的直线y=kx+b与直线y=4x+2相交于点A(-2,-2),则不等式4x+2<kx+b<0的解集为-4<x<-2.
如图,经过点B(-4,0)的直线y=kx+b与直线y=4x+2相交于点A(-2,-2),则不等式4x+2<kx+b<0的解集为-4<x<-2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com