
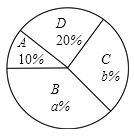
【题目】在“五四青年节”来临之际,某校举办了以“我的青春我做主”为主题的演讲比赛.并从参加比赛的学生中随机抽取部分学生的演讲成绩进行统计(等级记为![]() :优秀,
:优秀,![]() :良好,
:良好,![]() :一般,
:一般,![]() :较差),并制作了如下统计图表(部分信息未给出).
:较差),并制作了如下统计图表(部分信息未给出).
等级 | 人数 |
|
|
| 20 |
|
|
| 10 |
请根据统计图表中的信息解答下列问题:
(1)这次共抽取了______名参加演讲比赛的学生,统汁图中![]() ________,
________,![]() _______;
_______;
(2)求扇形统计图中演讲成绩等级为“一般”所对应扇形的圆心角的度数;
(3)若该校学生共2000人,如果都参加了演讲比赛,请你估计成绩达到优秀的学生有多少人?
(4)若演讲比赛成绩为![]() 等级的学生中恰好有2名女生,其余的学生为男生,从
等级的学生中恰好有2名女生,其余的学生为男生,从![]() 等级的学生中抽取两名同学参加全市演讲比赛,请用列表或画树状图的方法求出“恰好抽中—名男生和一名女生”的概率.
等级的学生中抽取两名同学参加全市演讲比赛,请用列表或画树状图的方法求出“恰好抽中—名男生和一名女生”的概率.
【答案】(1)50,40,30;(2)![]() ;(3)200人;(4)
;(3)200人;(4)![]()
【解析】
(1)根据D等级的人数和对应百分比可得抽取的人数,再分别求得等级B的人数所占百分比和等级C的人数所占百分比即可得出a,b的值;
(2)扇形统计图中演讲成绩等级为“一般”的为C类,所对应扇形的圆心角的度数为:![]()
(3)用等级A的人数所占百分比乘以2000即可
(4)用列表法列出所有情况,再根据概率公式即可求得
(1)这次抽取的演讲比赛的学生人数为10÷20%=50(名)
等级B的学生所占百分比为:![]() ×100%=40%
×100%=40%
∴a=40
等级C的学生所占百分比为110%20%40%=30%
∴b=30
故答案为:50,40,30
(2)扇形统计图中演讲成绩等级为“一般”的为C类,所对应扇形的圆心角的度数为:
![]()
故答案为:![]()
(3)估计成绩达到优秀的人数为:2000×10%=200(人)
故答案为:200人
(4)A等级的学生共有50×10%=5(名),其中有2名女生,那么男生有3名,
列表分析如下:
女1 | 女2 | 男1 | 男2 | 男3 | |
女1 | 女1女2 | 女1男1 | 女1男2 | 女1男3 | |
女2 | 女2女1 | 女2男1 | 女2男2 | 女2男3 | |
男1女1 | 男1女2 | 男1男2 | 男1男3 | ||
男2 | 男2女1 | 男2女2 | 男2男1 | 男2男3 | |
男3 | 男3女1 | 男3女2 | 男3男1 | 男3男2 |
由上表可知,一共有20种等可能的结果,其中抽中一名男生和一名女生的结果有12种,
则P(抽中一名男生和一名女生)=![]()
故答案为:![]()


科目:初中数学 来源: 题型:
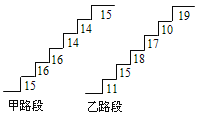
【题目】在某旅游景区上山的一条小路上,有一些断断续续的台阶,下图是其中的甲、乙两段台阶的示意图,图中的数字表示每一级台阶的高度(单位:cm).请你用所学过的有关统计知识,回答下列问题(数据:15,16,16,14,14,15的方差![]() ,数据:11,15,18,17,10,19的方差
,数据:11,15,18,17,10,19的方差![]() :
:
(1)分别求甲、乙两段台阶的高度平均数;
(2)哪段台阶走起来更舒服?与哪个数据(平均数、中位数、方差和极差)有关?
(3)为方便游客行走,需要陈欣整修上山的小路,对于这两段台阶路.在总高度及台阶数不变的情况下,请你提出合理的整修建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展了“创建文明校园”活动周,活动周设置了“A:文明礼仪,B:生态环境,C:交通安全,D:卫生保洁”四个主题,每个学生选一个主题参与.为了解活动开展情况,学校随机抽取了部分学生进行调查,并根据调查结果绘制了如下条形统计图和扇形统计图.
(1)本次随机调查的学生人数是 人;
(2)请你补全条形统计图;
(3)在扇形统计图中,“A”所在扇形的圆心角等于 度;
(4)小明和小华各自随机参加其中的一个主题活动,请用画树状图或列表的方式,求他们恰好同时选中“文明礼仪”或“生态环境”主题的概率.


查看答案和解析>>
科目:初中数学 来源: 题型:
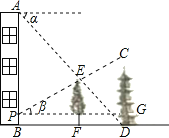
【题目】如图,在一居民楼AB和塔CD之间有一棵树EF,从楼顶A处经过树顶E点恰好看到塔的底部D点,且俯角α为38°.从距离楼底B点2米的P处经过树顶E点恰好看到塔的顶部C点,且仰角β为28°.已知树高EF=8米,求塔CD的高度.(参考数据:sin38°≈0.6,cos38°≈0.8,tan38°≈0.8,sin28°≈0.5,cos28°≈0.9,tan28°≈0.5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知圆锥的高为![]() ,母线为
,母线为![]() ,且
,且![]() ,圆锥的侧面展开图为如图所示的扇形.将扇形沿
,圆锥的侧面展开图为如图所示的扇形.将扇形沿![]() 折叠,使
折叠,使![]() 点恰好落在
点恰好落在![]() 上的
上的![]() 点,则弧长
点,则弧长![]() 与圆锥的底面周长的比值为( )
与圆锥的底面周长的比值为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,![]() //
//![]() ,且分别交对角线AC于点E,F,连接BE,DF.
,且分别交对角线AC于点E,F,连接BE,DF.

(1)求证:AE=CF;
(2)若BE=DE,求证:四边形EBFD为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形的边长为1的网格中,A,B,D,E为格点,C为![]() ,
,![]() 的延长线的交点.
的延长线的交点.
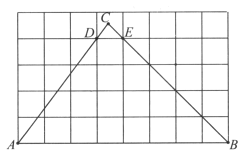
(Ⅰ)![]() 的结果为_________________.
的结果为_________________.
(Ⅱ)若点R在线段![]() 上,点S在线段
上,点S在线段![]() 上,点T在线段
上,点T在线段![]() 上,且满足四边形
上,且满足四边形![]() 为菱形,请在如图所示的网格中,用无刻度的直尺,画出菱形
为菱形,请在如图所示的网格中,用无刻度的直尺,画出菱形![]() ,并简要说明点R,S,T的位置是如何找到的(不要求证明)____________________.
,并简要说明点R,S,T的位置是如何找到的(不要求证明)____________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com