
”¾ĢāÄæ”æČēĶ¼£¬ŌŚŹżÖįÉĻµć![]() ±ķŹ¾Źż
±ķŹ¾Źż![]() £¬µć
£¬µć![]() ±ķŹ¾Źż
±ķŹ¾Źż![]() £¬µć
£¬µć![]() ±ķŹ¾Źż
±ķŹ¾Źż![]() £¬ĒŅµć
£¬ĒŅµć![]() ŌŚµć
ŌŚµć![]() µÄ×ó²ą£¬Ķ¬Ź±
µÄ×ó²ą£¬Ķ¬Ź±![]() ”¢
”¢![]() Āś×ć
Āś×ć![]() £¬
£¬![]() £®
£®
![]()
£Ø1£©ÓÉĢāŅā£ŗ![]() ______£¬
______£¬![]() ______£¬
______£¬![]() ______£»
______£»
£Ø2£©µ±µć![]() ŌŚŹżÖįÉĻŌĖ¶ÆŹ±£¬µć
ŌŚŹżÖįÉĻŌĖ¶ÆŹ±£¬µć![]() µ½
µ½![]() ”¢
”¢![]() Į½µć¾ąĄėÖ®ŗĶµÄ×īŠ”ÖµĪŖ______£®
Į½µć¾ąĄėÖ®ŗĶµÄ×īŠ”ÖµĪŖ______£®
£Ø3£©¶Æµć![]() ”¢
”¢![]() ·Ö±š“Óµć
·Ö±š“Óµć![]() ”¢
”¢![]() ŃŲŹżÖįøŗ·½ĻņŌČĖŁŌĖ¶ÆĶ¬Ź±³ö·¢£¬µć
ŃŲŹżÖįøŗ·½ĻņŌČĖŁŌĖ¶ÆĶ¬Ź±³ö·¢£¬µć![]() µÄĖŁ¶ČŹĒĆæĆė
µÄĖŁ¶ČŹĒĆæĆė![]() øöµ„Ī»³¤¶Č£¬µć
øöµ„Ī»³¤¶Č£¬µć![]() µÄĖŁ¶ČŹĒĆæĆė2øöµ„Ī»³¤¶Č£¬ĒóŌĖ¶Æ¼øĆėŗó£¬
µÄĖŁ¶ČŹĒĆæĆė2øöµ„Ī»³¤¶Č£¬ĒóŌĖ¶Æ¼øĆėŗó£¬![]() £æ
£æ
£Ø4£©ŌŚŹżÖįÉĻÕŅŅ»µć![]() £¬Ź¹µć
£¬Ź¹µć![]() µ½
µ½![]() ”¢
Ӣ![]() Ӣ
”¢![]() ČżµćµÄ¾ąĄėÖ®ŗĶµČÓŚ10£¬ĒėÖ±½ÓŠ“³öĖłÓŠµÄµć
ČżµćµÄ¾ąĄėÖ®ŗĶµČÓŚ10£¬ĒėÖ±½ÓŠ“³öĖłÓŠµÄµć![]() ¶ŌÓ¦µÄŹż£®£Ø²»±ŲĖµĆ÷ĄķÓÉ£©
¶ŌÓ¦µÄŹż£®£Ø²»±ŲĖµĆ÷ĄķÓÉ£©
”¾“š°ø”æ£Ø1£©-1£»5£»-2£»£Ø2£©6£»£Ø3£©ŌĖ¶Æ![]() Ćė»ņ
Ćė»ņ![]() ĆėŹ±£¬
ĆėŹ±£¬![]() £»£Ø4£©2»ņ
£»£Ø4£©2»ņ![]() £®
£®
”¾½āĪö”æ
£Ø1£©øł¾Ż¾ų¶ŌÖµµÄ·ĒøŗŠŌ¼“æÉĒó³öa”¢bµÄÖµ£¬Č»ŗóøł¾ŻBCµÄ³¤ŗĶB”¢CµÄĻą¶ŌĪ»ÖĆ¼“æÉĒó³öc£»
£Ø2£©ĻČĒó³öABµÄ³¤£¬Č»ŗóøł¾ŻMµćŌŚŹżÖįÉĻµÄĪ»ÖĆ·ÖĄąĢÖĀŪ£¬·Ö±š»³ö¶ŌÓ¦µÄĶ¼ŠĪ£¬Č»ŗóøł¾ŻŹżÖį¼“æɽā“š£»
£Ø3£©ÉčtĆėŹ±£¬![]() £¬øł¾ŻµćP”¢µćQŌŚµćOµÄ²»Ķ¬Ī»ÖĆ·ÖĄąĢÖĀŪ£¬·Ö±š»³öĶ¼ŠĪ£¬ÓĆŗ¬Ź±¼ätµÄŹ½×Ó±ķŹ¾P”¢QŌĖ¶ÆµÄĀ·³Ģ£¬Č»ŗóøł¾ŻĢāŅāÖŠŅŃÖŖµČŹ½ĮŠ³ö·½³Ģ¼“æÉĒó³öt£»
£¬øł¾ŻµćP”¢µćQŌŚµćOµÄ²»Ķ¬Ī»ÖĆ·ÖĄąĢÖĀŪ£¬·Ö±š»³öĶ¼ŠĪ£¬ÓĆŗ¬Ź±¼ätµÄŹ½×Ó±ķŹ¾P”¢QŌĖ¶ÆµÄĀ·³Ģ£¬Č»ŗóøł¾ŻĢāŅāÖŠŅŃÖŖµČŹ½ĮŠ³ö·½³Ģ¼“æÉĒó³öt£»
£Ø4£©ÉčµćN¶ŌÓ¦µÄŹżĪŖx£¬Č»ŗóøł¾ŻNµćŌŚŹżÖįÉĻµÄĪ»ÖĆ·ÖĄąĢÖĀŪ£¬·Ö±š»³ö¶ŌÓ¦µÄĶ¼ŠĪ£¬Č»ŗóøł¾ŻŹżÖįÉĻĮ½µćµÄ¾ąĄė¹«Ź½·Ö±šÓĆŗ¬xµÄŹ½×Ó±ķŹ¾³öNA”¢NB”¢NC£¬ŌŁøł¾ŻŅŃÖŖĢõ¼žĮŠ·½³Ģ¼“æÉĒó³öN¶ŌÓ¦µÄŹż£»
½ā£ŗ£Ø1£©”ß![]() £¬
£¬![]()
”ą![]()
½āµĆ£ŗ![]() £¬
£¬![]() £»
£»
”ßµć![]() ŌŚµć
ŌŚµć![]() µÄ×ó²ą£¬
µÄ×ó²ą£¬![]()
”ą![]()
¹Ź“š°øĪŖ£ŗ-1£»5£»-2£»
£Ø2£©øł¾ŻŹżÖįæÉÖŖ£ŗAB=5££Ø-1£©=6
¢Łµ±µćMŌŚµćA×ó²ąŹ±£¬ČēĻĀĶ¼ĖłŹ¾
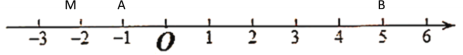
ÓÉŹżÖįæÉÖŖ£ŗ“ĖŹ±MA£«MB£¾AB=6£»
¢Śµ±µćMŌŚĻ߶ĪABÉĻŹ±£¬ČēĻĀĶ¼ĖłŹ¾
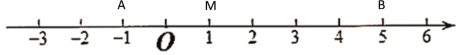
ÓÉŹżÖįæÉÖŖ£ŗ“ĖŹ±MA£«MB=AB=6£»
¢Ūµ±µćMŌŚµćBÓŅ²ąŹ±£¬ČēĻĀĶ¼ĖłŹ¾
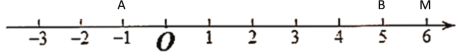
ÓÉŹżÖįæÉÖŖ£ŗ“ĖŹ±MA£«MB£¾AB=6£»
×ŪÉĻĖłŹö£ŗMA£«MB”Ż6
”ąµć![]() µ½
µ½![]() ”¢
”¢![]() Į½µć¾ąĄėÖ®ŗĶµÄ×īŠ”ÖµĪŖ6£®
Į½µć¾ąĄėÖ®ŗĶµÄ×īŠ”ÖµĪŖ6£®
£Ø3£©ÉčtĆėŹ±£¬![]() £¬·ÖĮ½ÖÖĒéæö£ŗ
£¬·ÖĮ½ÖÖĒéæö£ŗ
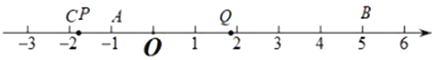
£Øi£©µ±µć![]() ŌŚµć
ŌŚµć![]() µÄ×ó²ą£¬µć
µÄ×ó²ą£¬µć![]() ŌŚµć
ŌŚµć![]() µÄÓŅ²ąŹ±£¬£ØČēŹ¾ŅāĶ¼£©
µÄÓŅ²ąŹ±£¬£ØČēŹ¾ŅāĶ¼£©
ÓÉĢāŅā£ŗ![]() £¬
£¬![]()
ӧ![]()
”ą![]()
½āµĆ£ŗ![]()
”ąµ±![]() Ź±£¬
Ź±£¬![]()
£Ø¢¢£©µ±µć![]() ”¢
”¢![]() ¾łŌŚŌŚµć
¾łŌŚŌŚµć![]() µÄ×ó²ąŹ±£¬ČēĻĀĶ¼ĖłŹ¾
µÄ×ó²ąŹ±£¬ČēĻĀĶ¼ĖłŹ¾
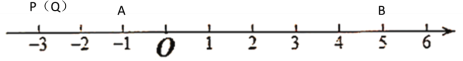
Čō![]() £¬Ōņµć
£¬Ōņµć![]() ”¢
”¢![]() ÖŲŗĻ£¬¼“
ÖŲŗĻ£¬¼“![]()
“ĖŹ±![]()
¼“![]()
½āµĆ£ŗ![]()
×ŪÉĻĖłŹö£ŗµ±![]() Ćė»ņ
Ćė»ņ![]() ĆėŹ±£¬
ĆėŹ±£¬![]()
“š£ŗŌĖ¶Æ![]() Ćė»ņ
Ćė»ņ![]() ĆėŹ±£¬
ĆėŹ±£¬![]() £®
£®
£Ø4£©ÉčµćN¶ŌÓ¦µÄŹżĪŖx£¬·ÖŅŌĻĀĖÄÖÖĒéæö
¢ŁČōµćNŌŚµćC×ó²ąŹ±£¬¼“x£¼-2Ź±£¬ČēĻĀĶ¼ĖłŹ¾£ŗ
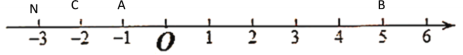
“ĖŹ±NC=-2£x£¬NA=-1£x£¬NB=5£x
øł¾ŻĢāŅāæÉÖŖ£ŗNA£«NB£«NC=10
¼“£Ø-1£x£©£«5£x£«£Ø-2£x£©=10
½āµĆ£ŗx=![]() £»
£»
¢ŚČōµćNŌŚµćCŗĶµćAÖ®¼äŹ±£¬¼“-2”Üx£¼-1Ź±£¬ČēĻĀĶ¼ĖłŹ¾£ŗ

“ĖŹ±NC=x££Ø-2£©=x£«2£¬NA=-1£x£¬NB=5£x
øł¾ŻĢāŅāæÉÖŖ£ŗNA£«NB£«NC=10
¼“£Ø-1£x£©£«5£x£«£Øx£«2£©=10
½āµĆ£ŗx=![]() £¬²»·ūŗĻĒ°ĢįĢõ¼ž£¬¹ŹÉįČ„£»
£¬²»·ūŗĻĒ°ĢįĢõ¼ž£¬¹ŹÉįČ„£»
¢ŪČōµćNŌŚµćAŗĶµćBÖ®¼äŹ±£¬¼“-1”Üx£¼5Ź±£¬ČēĻĀĶ¼ĖłŹ¾£ŗ
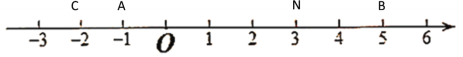
“ĖŹ±NC=x££Ø-2£©=x£«2£¬NA= x££Ø-1£©=x£«1£¬NB=5£x
øł¾ŻĢāŅāæÉÖŖ£ŗNA£«NB£«NC=10
¼“£Øx£«1£©£«5£x£«£Øx£«2£©=10
½āµĆ£ŗx=![]() £»
£»
¢ÜČōµćNŌŚµćBÓŅ²ąŹ±£¬¼“x£¾5Ź±£¬ČēĻĀĶ¼ĖłŹ¾£ŗ
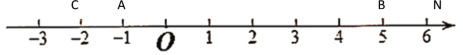
“ĖŹ±NC=x££Ø-2£©=x£«2£¬NA= x££Ø-1£©=x£«1£¬NB= x£5
øł¾ŻĢāŅāæÉÖŖ£ŗNA£«NB£«NC=10
¼“£Øx£«1£©£«x£5£«£Øx£«2£©=10
½āµĆ£ŗx=![]() £¬²»·ūŗĻĒ°ĢįĢõ¼ž£¬¹ŹÉįČ„£®
£¬²»·ūŗĻĒ°ĢįĢõ¼ž£¬¹ŹÉįČ„£®
×ŪÉĻĖłŹö£ŗĖłÓŠµÄµć![]() ¶ŌÓ¦µÄŹż£ŗ2»ņ
¶ŌÓ¦µÄŹż£ŗ2»ņ![]() £®
£®


 »ĘøŌ““ÓžķĻµĮŠ“š°ø
»ĘøŌ““ÓžķĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼ĖłŹ¾£¬ŌŚĢŻŠĪABCDÖŠ£¬AD”ĪBC£¬AB£½AD£¬”ĻBADµÄĘ½·ÖĻßAE½»BCÓŚµćE£¬Į¬½ÓDE£®
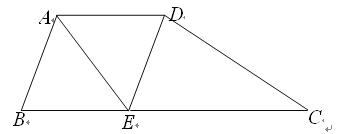
£Ø1£©ĒóÖ¤£ŗĖıߊĪABEDŹĒĮāŠĪ£»
£Ø2£©Čō”ĻABC£½60”ć£¬CE£½2BE£¬ŹŌÅŠ¶Ļ”÷CDEµÄŠĪד£¬²¢ĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬![]() ŹĒ
ŹĒ![]() µÄ½ĒĘ½·ÖĻߣ¬
µÄ½ĒĘ½·ÖĻߣ¬![]() £¬
£¬![]() ŹĒ
ŹĒ![]() µÄ½ĒĘ½·ÖĻߣ¬
µÄ½ĒĘ½·ÖĻߣ¬![]()
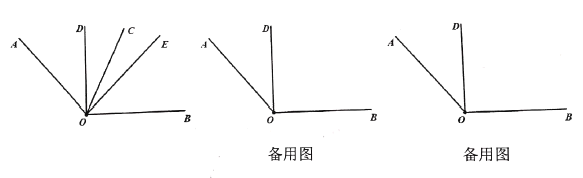
£Ø1£©Ēó![]() £»
£»
£Ø2£©![]() ČĘ
ČĘ![]() µćŅŌĆæĆė
µćŅŌĆæĆė![]() µÄĖŁ¶ČÄꏱÕė·½ĻņŠż×Ŗ
µÄĖŁ¶ČÄꏱÕė·½ĻņŠż×Ŗ![]() Ćė£Ø
Ćė£Ø![]() £©£¬
£©£¬![]() ĪŖŗĪÖµŹ±
ĪŖŗĪÖµŹ±![]() £»
£»
£Ø3£©ÉäĻß![]() ČĘ
ČĘ![]() µćŅŌĆæĆė
µćŅŌĆæĆė![]() µÄĖŁ¶ČÄꏱÕė·½ĻņŠż×Ŗ£¬ÉäĻß
µÄĖŁ¶ČÄꏱÕė·½ĻņŠż×Ŗ£¬ÉäĻß![]() ČĘ
ČĘ![]() µćŅŌĆæĆė
µćŅŌĆæĆė![]() µÄĖŁ¶ČĖ³Ź±Õė·½ĻņŠż×Ŗ£¬ČōÉäĻß
µÄĖŁ¶ČĖ³Ź±Õė·½ĻņŠż×Ŗ£¬ČōÉäĻß![]() Ķ¬Ź±æŖŹ¼Šż×Ŗ
Ķ¬Ź±æŖŹ¼Šż×Ŗ![]() Ćė£Ø
Ćė£Ø![]() £©ŗóµĆµ½
£©ŗóµĆµ½![]() £¬Ēó
£¬Ēó![]() µÄÖµ£®
µÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Ņ»“ĪŗÆŹży=kx+b£Øk”Ł0£©µÄĶ¼ĻóÓė·“±ČĄżŗÆŹż![]() £Øm”Ł0£©µÄĶ¼Ļó½»ÓŚA”¢BĮ½µć£¬ÓėxÖį½»ÓŚCµć£¬µćAµÄ×ų±źĪŖ£Øn£¬6£©£¬µćCµÄ×ų±źĪŖ£Ø©2£¬0£©£¬ĒŅtan”ĻACO=2£®
£Øm”Ł0£©µÄĶ¼Ļó½»ÓŚA”¢BĮ½µć£¬ÓėxÖį½»ÓŚCµć£¬µćAµÄ×ų±źĪŖ£Øn£¬6£©£¬µćCµÄ×ų±źĪŖ£Ø©2£¬0£©£¬ĒŅtan”ĻACO=2£®
£Ø1£©ĒóøĆ·“±ČĄżŗÆŹżŗĶŅ»“ĪŗÆŹżµÄ½āĪöŹ½£»
£Ø2£©ĒóµćBµÄ×ų±ź£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬ŅŃÖŖ”÷ABCČżøö¶„µćµÄ×ų±ź·Ö±šŹĒA£Ø2£¬2£©£¬B£Ø4£¬0£©£¬C£Ø4£¬©4£©£®
£Ø1£©ĒėŌŚĶ¼ÖŠ£¬»³ö”÷ABCĻņ×óĘ½ŅĘ6øöµ„Ī»³¤¶ČŗóµĆµ½µÄ”÷A1B1C1£»
£Ø2£©ŅŌµćOĪŖĪ»ĖĘÖŠŠÄ£¬½«”÷ABCĖõŠ”ĪŖŌĄ“µÄ![]() £¬µĆµ½”÷A2B2C2£¬ĒėŌŚĶ¼ÖŠyÖįÓŅ²ą£¬»³ö”÷A2B2C2£¬²¢Ēó³ö”ĻA2C2B2µÄÕżĻŅÖµ£®
£¬µĆµ½”÷A2B2C2£¬ĒėŌŚĶ¼ÖŠyÖįÓŅ²ą£¬»³ö”÷A2B2C2£¬²¢Ēó³ö”ĻA2C2B2µÄÕżĻŅÖµ£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼1ŹĒŅ»øöÓŠĮ½øöŌ²ÖłŠĪ¹¹³ÉµÄČŻĘ÷£¬×īĻĀĆęµÄŌ²ÖłŠĪµ×Ćę°ė¾¶![]() ”£ŌČĖŁµŲĻņæÕČŻĘ÷ÄŚ×¢Ė®£¬Ė®Ćęø߶Č
”£ŌČĖŁµŲĻņæÕČŻĘ÷ÄŚ×¢Ė®£¬Ė®Ćęø߶Č![]() £Øµ„Ī»£ŗĆ×£©ÓėŹ±¼ä
£Øµ„Ī»£ŗĆ×£©ÓėŹ±¼ä![]() £Øµ„Ī»£ŗŠ”Ź±£©µÄ¹ŲĻµČēĶ¼2ĖłŹ¾”£
£Øµ„Ī»£ŗŠ”Ź±£©µÄ¹ŲĻµČēĶ¼2ĖłŹ¾”£

£Ø1£©ĒóĖ®Ćęø߶Č![]() ÓėŹ±¼ä
ÓėŹ±¼ä![]() µÄŗÆŹż¹ŲĻµŹ½£»
µÄŗÆŹż¹ŲĻµŹ½£»
£Ø2£©Ēó×¢Ė®µÄĖŁ¶Č£Øµ„Ī»£ŗĮ¢·½Ć×/Ć抔Ź±£©£¬²¢ĒóČŻĘ÷ÄŚĖ®µÄĢå»ż![]() Óė×¢Ė®Ź±¼ä
Óė×¢Ė®Ź±¼ä![]() µÄŗÆŹż¹ŲĻµŹ½£»
µÄŗÆŹż¹ŲĻµŹ½£»
£Ø3£©ĒóÉĻĆęŌ²ÖłµÄµ×Ćę°ė¾¶£Ø±ŚŗńŗöĀŌ²»¼Ę£©”£
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ę½ŠŠĖıߊĪABCDµÄ±ßOAŌŚxÖįÉĻ£¬½«Ę½ŠŠĖıߊĪŃŲ¶Ō½ĒĻßAC¶ŌÕŪ£¬AOµÄ¶ŌÓ¦Ļ߶ĪĪŖAD£¬ĒŅµćD£¬C£¬OŌŚĶ¬Ņ»ĢõÖ±ĻßÉĻ£¬ADÓėBC½»ÓŚµćE.
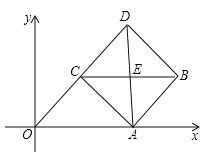
£Ø1£©ĒóÖ¤£ŗ”÷ABC”Õ”÷CDA.
£Ø2£©ČōÖ±ĻßABµÄŗÆŹż±ķ“ļŹ½ĪŖ![]() £¬ĒóČż½ĒĻßACEµÄĆ껿.
£¬ĒóČż½ĒĻßACEµÄĆ껿.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ¹ŲÓŚxµÄŅ»ŌŖ¶ž“Ī·½³Ģ![]() £ØmĪŖ³£Źż£©.
£ØmĪŖ³£Źż£©.
£Ø1£©Čē¹ū·½³ĢÓŠĮ½øö²»ĻąµČµÄŹµŹżøł£¬ĒómµÄȔֵ·¶Ī§.
£Ø2£©Čē¹ū·½³ĢÓŠĮ½øöĻąµČµÄŹµŹżøł£¬ĒómµÄÖµ”£
£Ø3£©Čē¹ū·½³ĢƻӊŹµŹżøł£¬ĒómµÄȔֵ·¶Ī§.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚŅ»Õų¤ĪŖ8cm£¬æķĪŖ6cmµÄ¾ŲŠĪÖ½Ę¬ÉĻ£¬ĻÖŅŖ¼ōĻĀŅ»øöŃü³¤ĪŖ5cmµÄµČŃüČż½ĒŠĪ£ØŅŖĒó£ŗµČŃüČż½ĒŠĪµÄŅ»øö¶„µćÓė¾ŲŠĪµÄŅ»øö¶„µćÖŲŗĻ£¬ĘäÓąµÄĮ½øö¶„µćŌŚ¾ŲŠĪµÄ±ßÉĻ£©£®Ōņ¼ōĻĀµÄµČŃüČż½ĒŠĪµÄĆ껿ĪŖ______cm2£®

²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com