
【题目】如图,在矩形ABCD中,E为CD的中点,F为BE上的一点,连接CF并延长交AB于点M,MN⊥CM交射线AD于点N
(1)如图1,当点F为BE的中点时,求证:AM=CE;
(2)如图2,若![]() =
=![]() =n(n≥3)时,请直接写出
=n(n≥3)时,请直接写出![]() 的值;
的值;
(3)若矩形ABCD(AB>BC)对角线AC交MN于T,H为边BC上一点,∠CMH=45°且![]() =
=![]() (如图3).若CF平分∠ACB,请直接写出
(如图3).若CF平分∠ACB,请直接写出![]() 的值.
的值.

【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)如图1中,证明△BFM≌△EFC(ASA)即可解决问题;
(2)如图2中,设BC=a,则AB=BC=na,EC=DE=![]() .利用相似三角形的性质求出EF,BF,根据EF:BF=n,构建方程求出n,求出AN,DN(用a表示),即可解决问题;
.利用相似三角形的性质求出EF,BF,根据EF:BF=n,构建方程求出n,求出AN,DN(用a表示),即可解决问题;
(3)如图3中,延长NM交CB的延长线于G,作CK⊥CM交MH的延长线于K,作KJ⊥BC于J.由△CBM≌△KJC(AAS),推出BM=CJ,BC=JK,设BM=CJ=x,由BH:CH=1:5,可以假设BH=x,CH=5x,由BM∥JK,推出![]() =
=![]() ,可得
,可得![]() =
=![]() ,解得x=3a或2a(舍弃),再想办法求出MF,MT即可解决问题.
,解得x=3a或2a(舍弃),再想办法求出MF,MT即可解决问题.
(1)证明:如图1中,
∵四边形ABCD是矩形,
∴AB=CD,AB∥CD,
∴∠MBF=∠CEF,
∵BF=EF,∠BFM=∠CFE,
在△BFM和△EFC中,
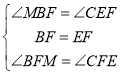 ,
,
∴△BFM≌△EFC(ASA),
∴BM=CE,
∵DE=EC=![]() CD,
CD,
∴BM=![]() AB,
AB,
∴AM=BM=EC.
(2)解:如图2中,设BC=a,则AB=CD=na,EC=DE=![]() .
.
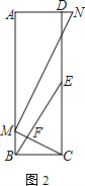
则EB=![]() ,
,
由CF⊥BE,可得EF=![]() =
=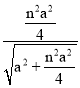 ,BF=
,BF=![]() =
=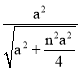 ,
,
∵EF:BF=n,
∴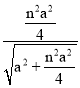 :
: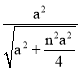 =n,
=n,
解得n=4或0(舍弃),
∴AB=DC=4a,EC=DE=2a,
易知BM=![]() a,AM=
a,AM=![]() a,AN=
a,AN=![]() a,DN=
a,DN=![]() a-a=
a-a=![]() a,
a,
∴![]() =
=![]() =
=![]() .
.
(3)解:如图3中,延长NM交CB的延长线于G,作CK⊥CM交MH的延长线于K,作KJ⊥BC于J.
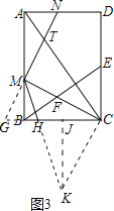
∵∠CMK=45°,∠MCK=90°,
∴CM=CK,
∵∠MCB+∠CMB=90°,∠MCB+∠BCK=90°,
∴∠CMB=∠BCK,
在△CBM和△KJC中,
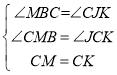 ,
,
易证△CBM≌△KJC(AAS),
∴BM=CJ,BC=JK,设BM=CJ=x,
∵BH:CH=1:5,
∴可以假设BH=x,CH=5x,
∵BM∥JK,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
解得x=3a或2a(舍弃),
∵CM平分∠ACB,易证![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴AC=2AM,设AM=y,则AC=2y,
∵AC2=AB2+BC2,
∴4y2=(y+3a)2+(6a)2,
解得y=5a(负根已经舍弃),
∴AM=5a,AB=CD=8a,EC=4a,CM=![]() =3
=3![]() a,
a,
∵BM∥EC,
∴![]() =
=![]() =
=![]() ,
,
∴MF=![]() ×3
×3![]() a=
a=![]() a,
a,
∵CM⊥TG,CM平分∠TCG,
∴易证MT=MG,
由△MBG∽△CBM,可得MG=![]() a,
a,
∴MT=![]() a,
a,
∴![]() =
=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E,D,连接EC,CD.
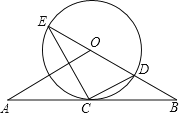
(1)求证:直线AB是⊙O的切线;
(2)若tan∠CED=![]() ,⊙O的半径为3,求OA的长.
,⊙O的半径为3,求OA的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上.

(1)画出△ABC关于原点对称的△A1B1C1;
(2)画出△ABC向上平移5个单位后的△A2B2C2,并求出平移过程中△ABC扫过的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() ,
,![]() 两点
两点![]() 在
在![]() 左侧),与
左侧),与![]() 轴交于点
轴交于点![]() ,顶点为
,顶点为![]() .
.
(1)当![]() 时,求四边形
时,求四边形![]() 的面积
的面积![]() ;
;
(2)在(1)的条件下,在第二象限抛物线对称轴左侧上存在一点![]() ,使
,使![]() ,求点
,求点![]() 的坐标;
的坐标;
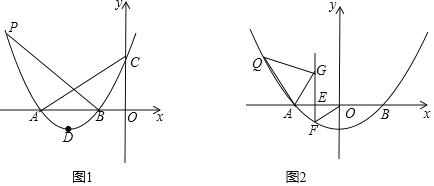
(3)如图2,将(1)中抛物线沿直线![]() 向斜上方向平移
向斜上方向平移![]() 个单位时,点
个单位时,点![]() 为线段
为线段![]() 上一动点,
上一动点,![]() 轴交新抛物线于点
轴交新抛物线于点![]() ,延长
,延长![]() 至
至![]() ,且
,且![]() ,若
,若![]() 的外角平分线交点
的外角平分线交点![]() 在新抛物线上,求
在新抛物线上,求![]() 点坐标.
点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=a(x-1)2+k与x轴两个交点间的距离为2,将抛物线y=a(x-1)2+k向上平移n个单位,平移后的抛物线经过点(m,n),则m的值是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学对全校学生进行文明礼仪知识测试,为了解测试结果,随机抽取部分学生的成绩进行分析,将成绩分为三个等级:不合格、一般、优秀,并绘制成如下两幅统计图(不完整).
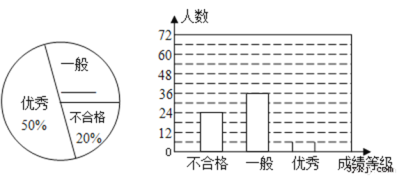
请你根据图中所给的信息解答下列问题:
(1)请将以上两幅统计图补充完整;
(2)若“一般”和“优秀”均被视为达标成绩,则该校被抽取的学生中有 人达标;
(3)若该校学生有1200人,请你估计此次测试中,全校达标的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数与x轴,y轴的交点分别是A(﹣4,0),B(0,2).与反比例函数的图象交于点Q,反比例函数图象上有一点P满足:①PA⊥x轴;②PO=![]() (O为坐标原点),则四边形PAQO的面积为( )
(O为坐标原点),则四边形PAQO的面积为( )

A.7B.10C.4+2![]() D.4﹣2
D.4﹣2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店在节日期间开展优惠促销活动:购买原价超过500元的商品,超过500元的部分可以享受打折优惠.若购买商品的实际付款金额y(单位:元)与商品原价x(单位:元)的函数关系的图像如图所示,则超过500元的部分可以享受的优惠是( )

A. 打六折B. 打七折C. 打八折D. 打九折
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,过
,过![]() ,
,![]() ,
,![]() 三点作圆,点
三点作圆,点![]() 在第一象限部分的圆上运动,连结
在第一象限部分的圆上运动,连结![]() ,过点
,过点![]() 作
作![]() 的垂线交
的垂线交![]() 的延长线于点
的延长线于点![]() ,下列说法:①
,下列说法:①![]() ;②
;②![]() ;③
;③![]() 的最大值为10.其中正确的是( )
的最大值为10.其中正确的是( )
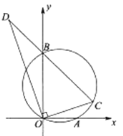
A. ①②B. ②③C. ①③D. ①②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com