
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��y=![]() ��������y=
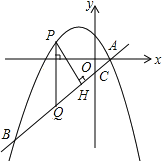
��������y=![]() ����A��B���㣬�ҵ�A��x���ϣ���B�ĺ�����Ϊ-4����PΪֱ��AB�Ϸ�����������һ���㣨�����A��B�غϣ�������P��x��Ĵ��߽�ֱ��AB�ڵ�Q��PH��AB��H��
����A��B���㣬�ҵ�A��x���ϣ���B�ĺ�����Ϊ-4����PΪֱ��AB�Ϸ�����������һ���㣨�����A��B�غϣ�������P��x��Ĵ��߽�ֱ��AB�ڵ�Q��PH��AB��H��
��1����b��ֵ��sin��PQH��ֵ��
��2�����P�ĺ�����Ϊt���ú�t�Ĵ���ʽ��ʾ��P��ֱ��AB�ľ���PH�ij��������PH֮�������ֵ�Լ���ʱt��ֵ��
��3������PB�����߶�PQ����PBH�ֳɳ���PQB����PQH�������ȣ����ʱ��P�����꣮
���𰸡���1��b=-1��![]() ����2��
����2��![]() ����t=-1ʱ��PH�����ֵΪ
����t=-1ʱ��PH�����ֵΪ![]() ����3��P��-3��0����
����3��P��-3��0����
��������
��1����y=0�������A�����꣬Ȼ��ѵ�A���������ֱ�߽���ʽ�������B��ֵ��Ȼ����ݵ�A�͵�C�����꣬���OA��OC�ij��ȣ����ݹ��ɶ������AC�ij��ȣ�����PQ��OC���ɵá�PQH=��OCA��Ȼ�����sin��PQH��ֵ��
��2�������P�͵�Q�����꣬�������Ǻ��������PH�ĺ�����ϵʽ�����������ֵ�ķ�����⼴�ɣ�
��3����BD��PQ��PQ���ӳ����ڵ�D����S��PQB=S��PQH���ó�BQ=QH���������Ǻ������QH��BQ�Ĺ�ϵʽ��������ȵĹ�ϵ���t�����ɵó���P�����꣮
�⣺��1����y=0�ã�![]() ������x2+x-6=0�����x1=-3��x2=2��
������x2+x-6=0�����x1=-3��x2=2��
��A��2��0����
��A��2��0����ֱ��![]() �ϣ�
�ϣ�
��1+b=0�����b=-1��
��OC=1��OA=2��
![]() ��
��
��PQ��OC��
���PQH=��OCA��
![]() ��
��
��2��![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
�൱t=-1ʱ��PH�����ֵΪ![]() ��
��
��3����ͼ����BD��PQ��PQ���ӳ����ڵ�D�����P�ĺ�����Ϊt��
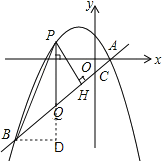
��S��PQB=S��PQH��
��BQ=QH��
��RT��PHQ��
![]() ��
��
![]() ��
��
![]() ��
��
��RT��BDQ��
�ߡ�BQD=��PQH��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
��t2+7t+12=0��
��t1=-3��t2=-4����ȥ����
��P��-3��0����


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
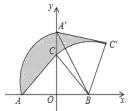
����Ŀ����ͼ��Rt��ABC�У���ACB��90�㣬AC��BC��2������AB���е�OΪ����ԭ�㣬AB����ֱ��Ϊx�Ὠ����ƽ��ֱ��������ϵ�У�����ABC�Ƶ�B˳ʱ����ת��ʹ��A��ת��y���������ϵ�A�䴦����ͼ����Ӱ�������Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��AOB��60�㣬�ڡ�AOB��ƽ����OM����һ��C����һ��120��ǵĶ������C�غϣ����������߷ֱ���ֱ��OA��OB�ཻ�ڵ�D��E��
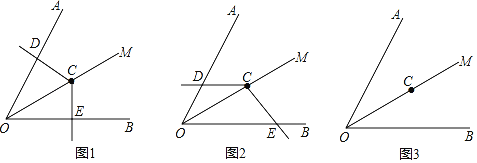
��1������DCE�Ƶ�C��ת��CD��OA��ֱʱ����ͼ1���������OE+OD��OC��������ϵ����˵�����ɣ�
��2������DCE�Ƶ�C��ת��CD��OA����ֱʱ������ͼ2��λ�ã���1���еĽ����Ƿ��������˵�����ɣ�
��3������DCE�Ƶ�C��ת��CD��OA�ķ����ӳ����ཻʱ�����������Ƿ����������ͼ3�л���ͼ�Σ��������������֤���������������߶�OD��OE��OC֮������������������ϵ����д����IJ��룬����֤��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ����У���ƻ������Ϊ400ƽ���Ļ�̳��������̻������ż��̶ӻ��ҹ��̶���ɣ���֪��ƽ��ÿ������̻���������Ҷӵ�2�������Ҽӱ��Ҷ�������4�����������ס��������̶�ƽ��ÿ��������̻�������ֱ��Ƕ���ƽ���ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ���mx2+��4-3m��x+2m-8=0��m��0����
��1����֤����������������ȵ�ʵ������
��2���跽�̵��������ֱ�Ϊx1��x2��x1��x2������n=x2-x1![]() m���ҵ�B��m��n����x���ϣ���m��ֵ��
m���ҵ�B��m��n����x���ϣ���m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ز�������һ��ˮ���������ÿǧ��40Ԫ����60Ԫ���ۣ�ƽ��ÿ�����100ǧ�ˣ����������г����鷢�֣�����ÿ����2Ԫ����ƽ��ÿ�������20ǧ��������
��1������ר�����������ֺ���Ҫ��ƽ��ÿ�����2240Ԫ��ÿǧ��ˮ��Ӧ������Ԫ��
��2������ר�����������ֺ���Ҫ��ƽ��ÿ��������ÿǧ��ˮ��Ӧ������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
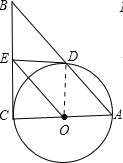
����Ŀ����ͼ����Rt��ABC�У���C=90������ACΪֱ������O����AB��D������O��OE��AB����BC��E��
��1����֤��EDΪ��O�����ߣ�
��2�������O�İ뾶Ϊ![]() ��ED=2���ӳ�EO����O��F������DF��AF������ADF�������
��ED=2���ӳ�EO����O��F������DF��AF������ADF�������

���𰸡���1��֤������������2��![]()
�������������������1����������OD����OE��AB������ƽ��������������ε����ʣ���֤��![]() ��
��![]() ���ɵ�
���ɵ�![]() �����֤��
�����֤��![]() Ϊ
Ϊ![]() �����ߣ�
�����ߣ�
��2������CD������ֱ�����Ե�Բ�ܽ���ֱ�ǣ����ɵ�![]() ���ù��ɶ����������
���ù��ɶ����������![]() �ij�������OE��AB��֤��
�ij�������OE��AB��֤��![]() �������������εĶ�Ӧ�߳ɱ������������
�������������εĶ�Ӧ�߳ɱ������������![]() �ij���Ȼ���������Ǻ�����֪ʶ�����
�ij���Ȼ���������Ǻ�����֪ʶ�����![]() ��
��![]() �ij���Ȼ������S��ADF=S����ABEF-S����DBEF��ô𰸣�
�ij���Ȼ������S��ADF=S����ABEF-S����DBEF��ô𰸣�
���������(1)֤��������OD��
��OE��AB��
���COE=��CAD����EOD=��ODA��
��OA=OD,
���OAD=��ODA��
���COE=��DOE��
�ڡ�COE�͡�DOE�У�
 ���COE�ա�DOE(SAS)��
���COE�ա�DOE(SAS)��
![]()
��ED��OD��
��ED��![]() �����ߣ�
�����ߣ�
(2)����CD����OE��M��
��Rt��ODE��
��OD=32��DE=2��
![]()
��OE��AB��
���COE�ס�CAB��
![]() ��AB=5��
��AB=5��
��AC��ֱ����
![]()
![]()
![]()
![]()
��EF��AB��
![]()
![]()
![]()
��S��ADF=S����ABEFS����DBEF
![]()
���ADF�����Ϊ![]()

�����͡������
��������
25
����Ŀ������Ŀ����֪��������y=ax2+ax+b��a��0����ֱ��y=2x+m��һ��������M��1��0������a��b��
��1����b��a�Ĺ�ϵʽ�������ߵĶ���D���꣨��a�Ĵ���ʽ��ʾ����
��2��ֱ���������ߵ�����һ�������ΪN������DMN�������a�Ĺ�ϵʽ��
��3��a=��1ʱ��ֱ��y=��2x���������ڵڶ������ڵ�G����G��H����ԭ��Գƣ��ֽ��߶�GH��y������ƽ��t����λ��t��0�������߶�GH����������������ͬ�Ĺ����㣬����t��ȡֵ��Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
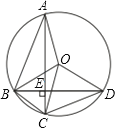
����Ŀ����ͼ���ڡ�O�У���AC��BD�ڵ�E������AB��CD��BC
��1����֤����AOB+��COD��180����
��2����AB��8��CD��6�����O��ֱ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
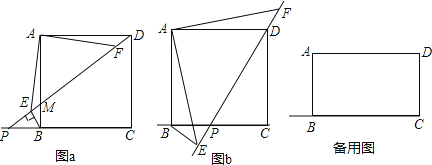
����Ŀ����ͼ��������ABCD����P������CB���˶�(��������B��C)������DP����AB�ڵ�M����BE��DP�ڵ�E������AE������FAD=��EAB��FA��DP�ڵ�F��
(1)��ͼa������P��CB���ӳ�����ʱ��
����֤��DF=BE��
�����ж�DE��BE��AE֮���������ϵ��֤����
(2)��ͼb������P���߶�BC��ʱ��DE��BE��AE֮����������������ϵ����ֱ��д���𰸣�����֤����
(3)�������֪�е�������ABCD���ɾ���ABCD����AD��AB=![]() ��1�������������䣬����P������CB��ʱ��DE��BE��AE֮������������������ϵ����ֱ��д���𰸣�����֤����
��1�������������䣬����P������CB��ʱ��DE��BE��AE֮������������������ϵ����ֱ��д���𰸣�����֤����
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com