
،¾جâؤ؟،؟زرضھ£؛ض±دكy=![]() x©پ3سëxضل،¢yضل·ض±ً½»سعµمA،¢B£¬إ×خïدكy=
x©پ3سëxضل،¢yضل·ض±ً½»سعµمA،¢B£¬إ×خïدكy=![]() x2+bx+c¾¹µمA،¢B£¬از½»xضلسعµمC£®
x2+bx+c¾¹µمA،¢B£¬از½»xضلسعµمC£®
£¨1£©اَإ×خïدكµؤ½âخِت½£»
£¨2£©µمPخھإ×خïدكةدز»µم£¬ازµمPشعABµؤدآ·½£¬ةèµمPµؤ؛ل×ّ±êخھm£®
¢ظتشاَµ±mخھ؛خضµت±£¬،÷PABµؤأو»×î´َ£»
¢عµ±،÷PABµؤأو»×î´َت±£¬¹µمP×÷xضلµؤ´¹دكPD£¬´¹×مخھµمD£¬ختشعض±دكPDةد·ٌ´وشعµمQ£¬ت¹،÷QBCخھض±½اب½اذخ£؟بô´وشع£¬ض±½سذ´³ِ·û؛دجُ¼µؤQµؤ×ّ±êبô²»´وشع£¬اëثµأ÷ہيسة£®
،¾´ً°¸،؟£¨1£©y=![]() x2©پ
x2©پ![]() x©پ3£»£¨2£©¢ظµ±m=3ت±£¬،÷PABµؤأو»×î´َ£¬×î´َضµتا9£¬¢عشعض±دكPDةد·ٌ´وشعµمQ£¨3£¬
x©پ3£»£¨2£©¢ظµ±m=3ت±£¬،÷PABµؤأو»×î´َ£¬×î´َضµتا9£¬¢عشعض±دكPDةد·ٌ´وشعµمQ£¨3£¬![]() £©»ٍ£¨3£¬©پ
£©»ٍ£¨3£¬©پ![]() £©£¬ت¹،÷QBCخھض±½اب½اذخ£®
£©£¬ت¹،÷QBCخھض±½اب½اذخ£®
،¾½âخِ،؟
£¨1£©ہûسأز»´خ؛¯تح¼دَةدµمµؤ×ّ±êجطص÷؟ةاَ³ِµمA،¢Bµؤ×ّ±ê£¬شظہûسأ´¶¨دµت·¨¼´؟ةاَ³ِإ×خïدكµؤ½âخِت½£»
£¨2£©¢ظ¹µمP×÷PD،حxضلسعD£¬½»ABسعµمE£¬ةèµمPµؤ؛ل×ّ±êخھm£¬شٍµمPµؤ×ّ±êخھ£¨m£¬![]() m2©پ
m2©پ![]() m©پ3£©£¬µمEµؤ×ّ±êخھ£¨m£¬
m©پ3£©£¬µمEµؤ×ّ±êخھ£¨m£¬![]() m©پ3£©£¬½ّ¶ّ؟ةµأ³ِPEµؤ³¤¶ب£¬شظہûسأب½اذخµؤأو»¹«ت½¼´؟ةµأ³ِS،÷PAB=©پm2+6m£¬ہûسأإن·½·¨¼´؟ة½â¾ِ×îضµختج⣻
m©پ3£©£¬½ّ¶ّ؟ةµأ³ِPEµؤ³¤¶ب£¬شظہûسأب½اذخµؤأو»¹«ت½¼´؟ةµأ³ِS،÷PAB=©پm2+6m£¬ہûسأإن·½·¨¼´؟ة½â¾ِ×îضµختج⣻
¢عہûسأ¶´خ؛¯تح¼دَةدµمµؤ×ّ±êجطص÷؟ةاَ³ِµمCµؤ×ّ±ê£¬ةèµمQµؤ×ّ±êخھ£¨3£¬y£©£¬شٍCQ2=£¨![]() £©2+y2£¬BC2=9+
£©2+y2£¬BC2=9+![]() £¬BQ2=9+£¨y+3£©2£¬·ض،دQCB=90،م،¢،دCBQ=90،م¼°،دCQB=90،مبضضاé؟ِ£¬ہûسأ¹´¹ة¶¨ہي¼´؟ةµأ³ِ¹طسعyµؤ·½³ج£¬½âض®¼´؟ةµأ³ِ½لآغ£®
£¬BQ2=9+£¨y+3£©2£¬·ض،دQCB=90،م،¢،دCBQ=90،م¼°،دCQB=90،مبضضاé؟ِ£¬ہûسأ¹´¹ة¶¨ہي¼´؟ةµأ³ِ¹طسعyµؤ·½³ج£¬½âض®¼´؟ةµأ³ِ½لآغ£®
£¨1£©،كض±دكy=![]() x©پ3سëxضل،¢yضل·ض±ً½»سعµمA،¢B£¬
x©پ3سëxضل،¢yضل·ض±ً½»سعµمA،¢B£¬
،àµمAµؤ×ّ±êخھ£¨6£¬0£©£¬µمBµؤ×ّ±êخھ£¨0£¬©پ3£©£®
½«A£¨6£¬0£©،¢B£¨0£¬©پ3£©´ْبëy=![]() x2+bx+c£¬µأ£؛
x2+bx+c£¬µأ£؛
![]() £¬½âµأ£؛
£¬½âµأ£؛ £¬
£¬
،àإ×خïدكµؤ½âخِت½خھy=![]() x2©پ
x2©پ![]() x©پ3£®
x©پ3£®
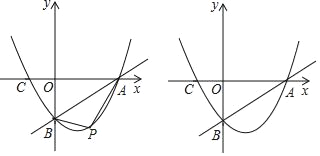
£¨2£©¢ظ¹µمP×÷PD،حxضلسعD£¬½»ABسعµمE£¬بçح¼1ثùت¾£®

ةèµمPµؤ؛ل×ّ±êخھm£¬شٍµمPµؤ×ّ±êخھ£¨m£¬![]() m2©پ
m2©پ![]() m©پ3£©£¬µمEµؤ×ّ±êخھ£¨m£¬
m©پ3£©£¬µمEµؤ×ّ±êخھ£¨m£¬![]() m©پ3£©£¬
m©پ3£©£¬
،àPE=![]() m©پ3©پ£¨
m©پ3©پ£¨![]() m2©پ
m2©پ![]() m©پ3£©=©پ
m©پ3£©=©پ![]() m2+2m£¬
m2+2m£¬
،àS،÷PAB=![]() ،ءPE،ء£¨AD+DO£©=
،ءPE،ء£¨AD+DO£©=![]() ،ء£¨©پ
،ء£¨©پ![]() m2+2m£©،ء6=©پm2+6m=©پ£¨m©پ3£©2+9£¬
m2+2m£©،ء6=©پm2+6m=©پ£¨m©پ3£©2+9£¬
،൱m=3ت±£¬،÷PABµؤأو»×î´َ£¬×î´َضµتا9£®
¢عµ±y=0ت±£¬سذ![]() x2©پ
x2©پ![]() x©پ3=0£¬
x©پ3=0£¬
½âµأ£؛x1=©پ![]() £¬x2=6£¬
£¬x2=6£¬
،àµمCµؤ×ّ±êخھ£¨©پ![]() £¬0£©£®
£¬0£©£®
ةèµمQµؤ×ّ±êخھ£¨3£¬y£©£¬
شٍCQ2=£¨![]() £©2+y2£¬BC2=9+
£©2+y2£¬BC2=9+![]() £¬BQ2=9+£¨y+3£©2£®
£¬BQ2=9+£¨y+3£©2£®
µ±،دQCB=90،مت±£¬سذCQ2+BC2=BQ2£¬
¼´£¨![]() £©2+y2+9+
£©2+y2+9+![]() =9+£¨y+3£©2£¬
=9+£¨y+3£©2£¬
½âµأ£؛y=![]() £»
£»
µ±،دCBQ=90،مت±£¬سذBC2+BQ2=CQ2£¬
¼´9+![]() +9+£¨y+3£©2=£¨
+9+£¨y+3£©2=£¨![]() £©2+y2£¬
£©2+y2£¬
½âµأ£؛y=©پ![]() £»
£»
µ±،دCQB=90،مت±£¬سذBQ2+CQ2=BC2£¬
¼´£¨![]() £©2+y2+9+£¨y+3£©2=9+
£©2+y2+9+£¨y+3£©2=9+![]() £¬
£¬
·½³جخق½â£®
×غةدثùت¾£؛شعض±دكPDةد·ٌ´وشعµمQ£¨3£¬![]() £©»ٍ£¨3£¬©پ
£©»ٍ£¨3£¬©پ![]() £©£¬ت¹،÷QBCخھض±½اب½اذخ£®
£©£¬ت¹،÷QBCخھض±½اب½اذخ£®



| ؤ꼶 | ¸كضذ؟خ³ج | ؤ꼶 | ³ُضذ؟خ³ج |
| ¸كز» | ¸كز»أâ·ر؟خ³جحئ¼ِ£، | ³ُز» | ³ُز»أâ·ر؟خ³جحئ¼ِ£، |
| ¸ك¶ | ¸ك¶أâ·ر؟خ³جحئ¼ِ£، | ³ُ¶ | ³ُ¶أâ·ر؟خ³جحئ¼ِ£، |
| ¸كب | ¸كبأâ·ر؟خ³جحئ¼ِ£، | ³ُب | ³ُبأâ·ر؟خ³جحئ¼ِ£، |
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟ذ،؛ى°ض°ض´س¼زئïµçئ؟³µ³ِ·¢£¬رطز»جُض±آ·µ½دà¾à2400mµؤر§ذ£½سذ،؛ى»ط¼ز£¬ذ،؛ى°ض°ض³ِ·¢µؤح¬ت±£¬ذ،؛ىزش96m/minµؤثظ¶ب´سر§ذ£رطح¬ز»جُµہآ·²½ذذ»ط¼ز£¬ذ،؛ى°ض°ض¸دµ½ر§ذ£ذ£أإ؟عµب؛ٍ2min؛َضھµہذ،؛ىزرہëذ££¬ء¢¼´رطشآ·زششثظ·µ»ط£¬ةèثûأا³ِ·¢µؤت±¼نخھt min£¬ح¼ت¾ضذµؤصغدكOABD±يت¾ذ،؛ى°ض°ضسë¼زض®¼نµؤ¾àہëS1سëtض®¼نµؤ؛¯ت¹طدµ£¬دك¶خEF±يت¾ذ،؛ىسë¼زض®¼نµؤ¾àہëS2سëtض®¼نµؤ؛¯ت¹طدµ£¬شٍذ،؛ى°ض°ض´س¼ز³ِ·¢شع·µ»طح¾ضذ×·ةدذ،؛ىµؤت±¼نتا£¨ £©
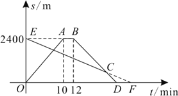
A.12minB.16minC.18minD.20min
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟شعئ½أوض±½ا×ّ±êدµ![]() ضذ£¬·´±بہ؛¯ت
ضذ£¬·´±بہ؛¯ت![]() µؤح¼دَ¾¹µم
µؤح¼دَ¾¹µم![]() £¬
£¬![]() £®
£®
£¨1£©اَ´ْتت½mnµؤضµ£»
£¨2£©بô¶´خ؛¯ت![]() µؤح¼دَ¾¹µمB£¬اَ´ْتت½
µؤح¼دَ¾¹µمB£¬اَ´ْتت½![]() µؤضµ£»
µؤضµ£»
£¨3£©بô·´±بہ؛¯ت![]() µؤح¼دَس붴خ؛¯ت
µؤح¼دَس붴خ؛¯ت![]() µؤح¼دَض»سذز»¸ِ½»µم£¬از¸أ½»µمشعض±دك
µؤح¼دَض»سذز»¸ِ½»µم£¬از¸أ½»µمشعض±دك![]() µؤدآ·½£¬½ل؛د؛¯تح¼دَ£¬اَ
µؤدآ·½£¬½ل؛د؛¯تح¼دَ£¬اَ![]() µؤب،ضµ·¶خ§£®
µؤب،ضµ·¶خ§£®

²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟شؤ¶ء£؛
¶شسعء½¸ِ²»µبµؤ·اءمتµت![]() £®بô·ضت½
£®بô·ضت½![]() µؤضµخھءم£¬شٍ
µؤضµخھءم£¬شٍ![]() »ٍ
»ٍ![]() سضزٍخھ
سضزٍخھ![]() £®ثùزش¹طسع
£®ثùزش¹طسع![]() µؤ·½³ج
µؤ·½³ج![]() سذء½¸ِ¸ù·ض±ًخھ
سذء½¸ِ¸ù·ض±ًخھ![]() £®
£®
س¦سأةدأوµؤ½لآغ½â´ًدآءذختجâ£؛
£¨1£©·½³ج![]() µؤء½¸ِ½âضذ½دذ،µؤز»¸ِخھ،،،،،،،،£®
µؤء½¸ِ½âضذ½دذ،µؤز»¸ِخھ،،،،،،،،£®
£¨2£©¹طسع½â![]() µؤ·½³ج
µؤ·½³ج![]() £¬ت×دبخزأاء½±كح¬¼س
£¬ت×دبخزأاء½±كح¬¼س![]() ³ة
³ة![]() £¬شٍ
£¬شٍ![]() »ٍ
»ٍ![]() £¬ء½¸ِ½â·ض±ًخھ
£¬ء½¸ِ½â·ض±ًخھ![]() £¬ شٍ
£¬ شٍ![]() £¬
£¬![]() £®
£®
£¨3£©¹طسع![]() µؤ·½³ج
µؤ·½³ج![]() µؤء½¸ِ½â·ض±ًخھ
µؤء½¸ِ½â·ض±ًخھ![]() £¬اَ
£¬اَ![]() µؤضµ£®
µؤضµ£®
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟خھءث½âؤ³تذاّ¾إؤ꼶ر§ةْأ؟جىµؤ½،ةي»î¶¯اé؟ِ£¬ثو»ْ´ستذاّ¾إؤ꼶µؤ12000أûر§ةْضذ³éب،ءث500أûر§ةْ£¬¶شصâذ©ر§ةْأ؟جىµؤ½،ةي»î¶¯ت±¼ن½ّذذح³¼ئصûہي£¬×÷³ِءثبçدآ²»حêصûµؤح³¼ئح¼£¨أ؟×éت¾ف؛¬×îذ،ضµ²»؛¬×î´َضµ£¬ح³¼ئت¾فب«²؟خھصûت£©£¬اë¸ù¾فزشدآذإد¢½â´ًبçدآختجâ£؛
ت±¼ن/·ض | ئµت | ئµآت |
30،«40 | 25 | 0.05 |
40،«50 | 50 | 0.10 |
50،«60 | 75 | b |
60،«70 | a | 0.40 |
70،«80 | 150 | 0.30 |
£¨1£©a=_______£¬b=_______£»
£¨2£©اë²¹ب«ئµت·ض²¼ض±·½ح¼£»
£¨3£©ر§ةْأ؟جى½،ةيت±¼نµؤضذخ»ت»لآنشعؤؤ¸ِت±¼ن¶خ£؟
£¨4£©بôأ؟جى½،ةيت±¼نشع60·ضضسزشةدخھ·û؛دأ؟جى،°رô¹âز»ذ،ت±،±µؤ¹و¶¨£¬شٍ·û؛د¹و¶¨µؤر§ةْبثت´َش¼تا¶àةظبث£؟

²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟![]() ¸غشع
¸غشع![]() µطµؤصؤد
µطµؤصؤد![]() ا§أ×´¦£¬ز»ثزآض´¬سة
ا§أ×´¦£¬ز»ثزآض´¬سة![]() ¸غ؟ھ³ِدٍخ÷؛½ذذ£¬ؤ³بثµعز»´خشع
¸غ؟ھ³ِدٍخ÷؛½ذذ£¬ؤ³بثµعز»´خشع![]() ´¦حû¼û¸أ´¬شعؤدئ«خ÷
´¦حû¼û¸أ´¬شعؤدئ«خ÷![]() £¬°ëذ،ت±؛َ£¬سضحû¼û¸أ´¬شعؤدئ«خ÷
£¬°ëذ،ت±؛َ£¬سضحû¼û¸أ´¬شعؤدئ«خ÷![]() £¬شٍ¸أ´¬ثظ¶بخھ________ا§أ×/ذ،ت±£®
£¬شٍ¸أ´¬ثظ¶بخھ________ا§أ×/ذ،ت±£®
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟ؤ³³¬تذش¤²âؤ³زûءد»ل³©دْ،¢دبسأ1800شھ¹؛½ّز»إْصâضضزûءد£¬أوتذ؛َ¹ûب»¹©²»س¦اَ£¬سضسأ8100شھ¹؛½ّصâضضزûءد£¬µع¶إْزûءدµؤتء؟تاµعز»إْµؤ3±¶£¬µ«µ¥¼غ±بµعز»إْ¹َ2شھ£®
£¨1£©µعز»إْزûءد½ّ»ُµ¥¼غ¶àةظشھ£؟
£¨2£©بôء½´خ½ّزûءد¶¼°´ح¬ز»¼غ¸ٌدْتغ£¬ء½إْب«²؟تغحê؛َ£¬»ٌہû²»ةظسع2700شھ£¬ؤاأ´دْتغµ¥¼غضءةظخھ¶àةظشھ£؟
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼ثùت¾£¬µمPتاµب±كب½اذخABCؤعµؤز»µم£¬ازPA=6£¬PB=8£¬PC=10£¬بô½«،÷PACبئµمAؤوت±صëذ×ھ؛َ£¬µأµ½،÷P،نAB£¬شٍ،دAPBµبسع£¨ £©
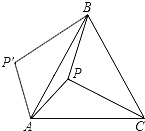
A£®150،م B£®105،م C£®120،م D£®90،م
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼£¬شع A ت±²âµأؤ³ت÷(´¹ض±سعµطأو)µؤس°³¤خھ 4 أ×£¬B ت±سض²âµأ¸أت÷µؤس°³¤خھ 16 أ×£¬بôء½´خبص صصµؤ¹âدك»¥دà´¹ض±£¬شٍت÷µؤ¸ك¶بخھ_____أ×£®
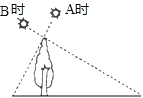
²é؟´´ً°¸؛ح½âخِ>>
°ظ¶بضآذإ - ء·د°²لءذ±ي - تشجâءذ±ي
؛±±ت،»¥ءھحّخ¥·¨؛ح²»ء¼ذإد¢¾ظ±¨ئ½ج¨ | حّةدسذ؛¦ذإد¢¾ظ±¨×¨اّ | µçذإص©ئ¾ظ±¨×¨اّ | ةوہْت·ذéخقض÷زهسذ؛¦ذإد¢¾ظ±¨×¨اّ | ةوئَاضب¨¾ظ±¨×¨اّ
خ¥·¨؛ح²»ء¼ذإد¢¾ظ±¨µç»°£؛027-86699610 ¾ظ±¨ستدن£؛58377363@163.com