
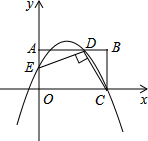
 如图,平面直角坐标系xOy中,矩形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=2,OC=3,AD=2,连接DC,过点D作DE⊥DC交OA于点E.
如图,平面直角坐标系xOy中,矩形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=2,OC=3,AD=2,连接DC,过点D作DE⊥DC交OA于点E.分析 (1)首先由矩形OABC的边OA在y轴的正半轴上,DE⊥DC,证得△ADE∽△BCD,然后由相似三角形的对应边成比例,求得AE的长,继而求得E的坐标;
(2)首先设过点E、D、C的抛物线的解析式为y=ax2+bx+c(a≠0),然后直接利用待定系数法求得此抛物线解析式;
(3)首先求得直线DM的解析式,然后过点D作DK⊥OC于点K,易证得△DAF≌△DKG,则可证得结论;
(4)分别从①若PG=PC,②若PG=GC,③若PC=GC,去分析求解即可求得答案.
解答 解:(1)∵四边形OABC是矩形,
∴∠EAD=∠B=90°,
∴∠AED+∠ADE=90°,
∵DE⊥DC,
∴∠ADE+∠BDC=90°,
∴∠AED=∠BDC,
∴△ADE∽△BCD,
∴AE:BD=AD:BC,
∵OA=2,OC=3,AD=2,
∴BC=OA=2,AB=OC=3,
∴BD=AB-AD=3-2=1,
∴AE:1=2:2,
解得:AE=1,
∴OE=OA-AE=1,
∴E(0,1);
故答案为:0,1;
(2)设过点E、D、C的抛物线的解析式为y=ax2+bx+c(a≠0),
将点E的坐标代入,得c=1.
将c=1和点D、C的坐标分别代入,得$\left\{\begin{array}{l}4a+2b+1=2\\ 9a+3b+1=0.\end{array}\right.$
解这个方程组,得$\left\{\begin{array}{l}a=-\frac{5}{6}\\ b=\frac{13}{6}\end{array}\right.$,
∴抛物线的解析式为:y=-$\frac{5}{6}$x2+$\frac{13}{6}$x+1.
(3)EF=2GO成立.
如图1,∵点M在该抛物线上,且它的横坐标为$\frac{6}{5}$,
∴点M的纵坐标为$\frac{12}{5}$.
设DM的解析式为y=kx+b1(k≠0),将
点D、M的坐标分别代入,得$\left\{\begin{array}{l}2k+{b_1}=2\\ \frac{6}{5}k+{b_1}=\frac{12}{5}.\end{array}\right.$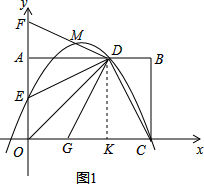
解得$\left\{\begin{array}{l}k=-\frac{1}{2}\\{b_1}=3\end{array}\right.$,
∴DM的解析式为:y=-$\frac{1}{2}$x+3.
∴F(0,3),
∴EF=2.
过点D作DK⊥OC于点K,则DA=DK.
∵∠ADK=∠FDG=90°,
∴∠FDA=∠GDK.
又∵∠FAD=∠GKD=90°,
在△DAF和△DKG中,
$\left\{\begin{array}{l}{∠FDA=∠GKD=90°}\\{DA=DK}\\{∠FDA=∠GDK}\end{array}\right.$,
∴△DAF≌△DKG.
∴KG=AF=1.
∴GO=1.
∴EF=2GO.
(3)如图2,∵点P在AB上,G(1,0),C(3,0),则设P(t,2).
∴PG2=(t-1)2+22,PC2=(3-t)2+22,GC=2.
①若PG=PC,则(t-1)2+22=(3-t)2+22,解得t=2.
∴P(2,2),此时点Q与点P重合.
∴Q(2,2).
②若PG=GC,则(t-1)2+22=22,解得 t=1,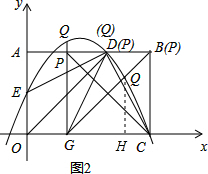 ∴P(1,2),此时GP⊥x轴.GP与该抛物线在第一象限内的交点Q的横坐标为1,
∴P(1,2),此时GP⊥x轴.GP与该抛物线在第一象限内的交点Q的横坐标为1,
∴点Q的纵坐标为$\frac{7}{3}$.
∴Q(1,$\frac{7}{3}$).
③若PC=GC,则(3-t)2+22=22,解得t=3,
∴P(3,2),此时PC=GC=2,
故△PCG是等腰直角三角形.
过点Q作QH⊥x轴于点H,则QH=GH,设QH=h,
∴Q(h+1,h).
∴-$\frac{5}{6}$(h+1)2+$\frac{13}{6}$(h+1)+1=h.
解得h1=$\frac{7}{5}$,h2═-2(舍去).
∴Q($\frac{12}{5}$,$\frac{7}{5}$).
综上所述,存在三个满足条件的点Q,即Q(2,2)或Q(1,$\frac{7}{3}$)或Q($\frac{12}{5}$,$\frac{7}{5}$).
点评 此题属于二次函数的综合题.考查了待定系数求函数解析式、正方形的性质、全等三角形的判定与性质、相似三角形的判定与性质以及等腰三角形的性质等知识.注意掌握分类讨论思想的应用,注意掌握辅助线的作法是解此题的关键,


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| 身高(cm) | 180 | 186 | 188 | 192 | 208 |
| 人数(个) | 4 | 6 | 5 | 3 | 2 |
| A. | 186,186 | B. | 186,187 | C. | 208,188 | D. | 188,187 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知函数C1:y=kx2+($\frac{4}{3}$-3k)x-4.
已知函数C1:y=kx2+($\frac{4}{3}$-3k)x-4.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | “面积相等的两个三角形全等”是必然事件 | |
| B. | “任意画一个等边三角形,它是轴对称图形”是随机事件 | |
| C. | “同位角相等”这一事件是不可能事件 | |
| D. | “三角形三条高所在直线的交点在三角形的外部”这一事件是随机事件 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 9% | B. | 10% | C. | 11% | D. | 12% |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com