
【题目】新华社消息:法国教育部宜布,小学和初中于2018年9月新学期开始,禁止学生在校使用手机.为了解学生手机使用情况,包河区某学校开展了“手机伴我健康行”的主题活动,学校随机抽取部分学生进行“使用手机的目的”和“每周使用手机的时间”的问卷调查,并绘制成如图①,图②的统计图.已知“查资料”的人数为40.

(1)本次抽样调查一共抽取了_________人;补全条形统计图;
(2)在扇形统计图中,“玩游戏”对应的圆心角的度数为_________度;
(3)该校共有学生2100人,请估计每周使用手机时间在2小时以上(不含2小时)的人数.
【答案】(1)100,图见解析;(2)126;(3)1344人.
【解析】
(1)根据题意可知“查资料”的人数为40,据此用40除以![]() 进行计算得出抽取人数,最后再算出其余时间人数以便补全条形统计图即可;
进行计算得出抽取人数,最后再算出其余时间人数以便补全条形统计图即可;
(2)先根据扇形图求出“玩游戏”所占的百分比,然后进一步乘以360°即可;
(3)先根据条形统计图求出每周使用手机时间在2小时以上(不含2小时)的人数占抽取人数的比值,然后乘以2100即可.
(1)抽取人数为:![]() (人),
(人),
∴“3小时以上”人数=![]() (人),
(人),
故答案为:100,补全的条形统计图如下:

(2)由扇形统计图得:“玩游戏”所占的百分比=![]() ,
,
∴“玩游戏”所占的圆心角度数=![]() °,
°,
故答案为:126;
(3)由条形统计图得:
每周使用手机时间在2小时以上(不含2小时)的人数占抽取人数的比值=![]() ,
,
∴![]() (人)
(人)
答:该校每周使用手机时间在2小时以上(不含2小时)的人数有1344人.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
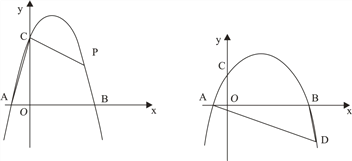
【题目】抛物线![]() 与x轴交于A,B两点(点A在点B的左边),与y轴正半轴交于点C.
与x轴交于A,B两点(点A在点B的左边),与y轴正半轴交于点C.
(1)如图1,若A(-1,0),B(3,0),
① 求抛物线![]() 的解析式;
的解析式;
② P为抛物线上一点,连接AC,PC,若∠PCO=3∠ACO,求点P的横坐标;
(2)如图2,D为x轴下方抛物线上一点,连DA,DB,若∠BDA+2∠BAD=90°,求点D的纵坐标.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
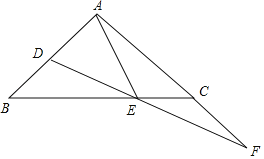
【题目】如图,△ABC中,AB=AC,∠BAC=90°,点D,E分别在AB,BC上,∠EAD=∠EDA,点F为DE的延长线与AC的延长线的交点.
(1)求证:DE=EF;
(2)判断BD和CF的数量关系,并说明理由;
(3)若AB=3,AE=![]() ,求BD的长.
,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
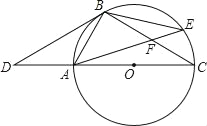
【题目】如图,点D是⊙O的直径CA延长线上一点,点B在⊙O上,且∠DBA=∠BCD.
(1)证明:BD是⊙O的切线.
(2)若点E是劣弧BC上一点,AE与BC相交于点F,且△BEF的面积为16,cos∠BFA=![]() ,那么,你能求出△ACF的面积吗?若能,请你求出其面积;若不能,请说明理由.
,那么,你能求出△ACF的面积吗?若能,请你求出其面积;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,最适合采用普查方式的是( )
A.了解三明市初中学生每天阅读的时间B.了解三明电视台“教育在线”栏目的收视率
C.了解一批节能灯的使用寿命D.了解某校七年级![]() 班同学的身高
班同学的身高
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,阶梯图的每个台阶上都标着一个数, 从下到上的第![]() 个至第
个至第![]() 个台阶上依次标着
个台阶上依次标着![]() ,且任意相邻四个台阶上的数的和都相等.
,且任意相邻四个台阶上的数的和都相等.

![]() 求前
求前![]() 个台阶上的数的和;
个台阶上的数的和;
![]() 求第
求第![]() 个台阶上的数x的值;
个台阶上的数x的值;
![]() 从下到上前
从下到上前![]() 为奇数)个台阶上的数的和能否为
为奇数)个台阶上的数的和能否为![]() ?若能,求出
?若能,求出![]() 的值;若不能,请说明理由.
的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究证明:
(1)如图1,在△ABC中,AB=AC,点E是BC上的一个动点,EG⊥AB,EF⊥AC,CD⊥AB,点G,F,D分别是垂足.求证:CD=EG+EF;
猜想探究:
(2)如图2,在△ABC中,AB=AC,点E是BC的延长线上的一个动点,EG⊥AB于G,EF⊥AC交AC延长线于F,CD⊥AB于D,直接猜想CD、EG、EF之间的关系为 CD=EG﹣EF ;
问题解决:
(3)如图3,边长为10的正方形ABCD的对角线相交于点O、H在BD上,且BH=BC,连接CH,点E是CH上一点,EF⊥BD于点F,EG⊥BC于点G,则EF+EG= .

查看答案和解析>>
科目:初中数学 来源: 题型:
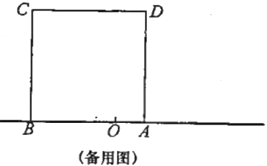
【题目】如图,已知数轴上点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为
表示的数为![]() ,以
,以![]() 为边在数轴的上方作正方形ABCD.动点
为边在数轴的上方作正方形ABCD.动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿数轴正方向匀速运动,同时动点
个单位长度的速度沿数轴正方向匀速运动,同时动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度向点
个单位长度的速度向点![]() 匀速运动,到达
匀速运动,到达![]() 点后再以同样的速度沿数轴正方向匀速运动,设运动时间为
点后再以同样的速度沿数轴正方向匀速运动,设运动时间为![]() 秒
秒![]() .
.
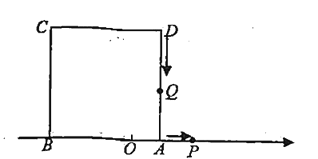
(1)若点![]() 在线段
在线段![]() .上运动,当t为何值时,
.上运动,当t为何值时,![]() ?
?
(2)若点![]() 在线段
在线段![]() 上运动,连接
上运动,连接![]() ,当t为何值时,三角形
,当t为何值时,三角形![]() 的面积等于正方形
的面积等于正方形![]() 面积的
面积的![]() ?
?
(3)在点![]() 和点
和点![]() 运动的过程中,当
运动的过程中,当![]() 为何值时,点
为何值时,点![]() 与点
与点![]() 恰好重合?
恰好重合?
(4)当点![]() 在数轴上运动时,是否存在某-时刻t,使得线段
在数轴上运动时,是否存在某-时刻t,使得线段![]() 的长为
的长为![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com