
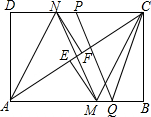
 如图,在矩形ABCD中,把∠B、∠D分别翻折,使点B、D分别落在对角线BC上的点E、F处,折痕分别为CM、AN.连接MF、NE. P、Q是矩形的边CD、AB上的两点,连结PQ、CQ、MN.若PQ=CQ,PQ∥MN,且AB=4,BC=3,则PC的长度是2.
如图,在矩形ABCD中,把∠B、∠D分别翻折,使点B、D分别落在对角线BC上的点E、F处,折痕分别为CM、AN.连接MF、NE. P、Q是矩形的边CD、AB上的两点,连结PQ、CQ、MN.若PQ=CQ,PQ∥MN,且AB=4,BC=3,则PC的长度是2. 分析 设AC与MN的交点为O,EF=x,作QG⊥PC于G点,首先求出AC=5,根据翻折变换知:AF=CE=3,于是可得AF+(CE-EF)=5,可得EF=1,在Rt△CFN中,NF=tan∠NCF•CF,在Rt△NFE中,NO2=NF2+OF2,求出NO的长,即NM=PQ=QC=2NO,PC=2$\sqrt{{PQ}^{2}-{QG}^{2}}$.
解答  解:设AC与MN的交点为O,EF=x,作QG⊥PC于G点,
解:设AC与MN的交点为O,EF=x,作QG⊥PC于G点,
∵AB=4,BC=3,
∴AC=5,
∵AF=CE=BC=3,
∴2AF-EF=AC,即6-x=5,
解得x=1,
∴EF=1,
∴CF=2,
在Rt△CFN中,tan∠DCA=$\frac{NF}{CF}$=$\frac{BC}{AB}$=$\frac{3}{4}$,
解得NF=$\frac{3}{2}$,
∵OE=OF=$\frac{1}{2}$EF=$\frac{1}{2}$,
∴在Rt△NFO中,ON2=OF2+NF2,
∴ON=$\frac{\sqrt{10}}{2}$,
∴MN=2ON=$\sqrt{10}$,
∵PQ∥MN,PN∥MQ,
∴四边形MQPN是平行四边形,
∴MN=PQ=$\sqrt{10}$,
∵PQ=CQ,
∴△PQC是等腰三角形,
∴PG=CG,
在Rt△QPG中,
PG2=PQ2-QG2,即PG=$\sqrt{10-9}$=1,
∴PC=2PG=2.
故答案为2.
点评 本题主要考查了翻折变换,还涉及平行四边形、菱形的证明,解答问的关键是求出EF的长,此题难度较大,要熟练掌握此类试题的解答,此类题经常出现中考试卷中,请同学们关注.


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:解答题
 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据图象信息解答:当出发几个小时后,两车相距为270km?
一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据图象信息解答:当出发几个小时后,两车相距为270km?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
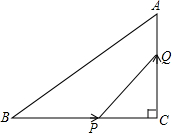 如图,△ABC中,∠C=90°,AC=3cm,BC=4cm,动点P从点B出发以2cm/s的速度向点C移动,同时动点Q从C出发以1cm/s的速度向点A移动,设它们的运动时间为t.
如图,△ABC中,∠C=90°,AC=3cm,BC=4cm,动点P从点B出发以2cm/s的速度向点C移动,同时动点Q从C出发以1cm/s的速度向点A移动,设它们的运动时间为t.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在四边形ABCD中,AD、BD相交于点F,点E在BD上,且$\frac{AB}{AE}$=$\frac{BC}{ED}$=$\frac{AC}{AD}$.
如图,在四边形ABCD中,AD、BD相交于点F,点E在BD上,且$\frac{AB}{AE}$=$\frac{BC}{ED}$=$\frac{AC}{AD}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知△ABC、△DCE、△FEG是三个全等的等腰三角形,底边BC、CE、EG在同一直线上,且AB=$\sqrt{3}$,BC=1.连接BF,分别交AC、DC、DE与点P、Q、R.有下列结论①△BFG∽△ABC、②BQ=FQ、③AP=2PC、④EF平分∠BFG,你认为不正确的是④.
如图,已知△ABC、△DCE、△FEG是三个全等的等腰三角形,底边BC、CE、EG在同一直线上,且AB=$\sqrt{3}$,BC=1.连接BF,分别交AC、DC、DE与点P、Q、R.有下列结论①△BFG∽△ABC、②BQ=FQ、③AP=2PC、④EF平分∠BFG,你认为不正确的是④.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
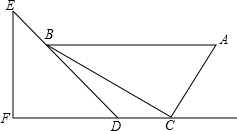 一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10.
一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com