练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

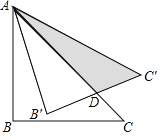
    【题目】如图，等腰直角三角形ABC的直角边AB的长为，将△ABC绕点A逆时针旋转15°后得到△AB′C′，AC与B′C′相交于点D，则图中阴影△ADC′的面积等于______．

    【答案】

    【解析】

    由旋转的性质可得AB=AB'=，∠BAB'=15°，可得∠B'AD=∠BAC-∠B'AB=30°，由直角三角形的性质可得B'D=1，由三角形面积公式可求解．

    解：∵AB=BC，∠ABC=90°，

    ∴∠BAC=45°，

    ∵△ABC绕点A逆时针旋转15°后得到△AB′C′，

    ∴AB=AB'=，∠BAB'=15°，

    ∴∠B'AD=∠BAC-∠B'AB=30°，且∠B'=90°，

    ∵tan∠B'AD=,

    ∴AB'=B'D，

    ∴B'D=1，

    ∴阴影△ADC'的面积=，

    故答案为：.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，池塘边有一块长为18米，宽为10米的长方形土地，现在将其余三面留出宽都是x米的小路，中间余下的长方形部分做菜地，用代数式表示：

    (1)菜地的长a=___米，宽b=___米；

    (2)菜地的面积S=___平方米；

    (3)求当x=1米时，菜地的面积。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

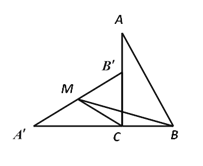
    【题目】如图，在Rt△ABC中，∠ACB = 90°，BC = 2．将△ABC绕顶点C逆时针旋转得到△使点落在AC边上．设M是的中点，连接BM，CM，则△BCM的面积为（ ）

    A. 1 B. 2 C. 3 D. 4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我们知道，|x|表示x在数轴上对应的点到原点的距离，我们可以把看作|x-0|，所以，|x- 3|就表示x在数轴上对应的点到3的距离，|x1||x-（-1）|就表示x在数轴上对应的点到-1的距离，由上面绝对值的几意义，解答下列问题：

    (1) 当|x-4||x2|有最小值时，x的取值情况是 ；

    (2) |x-3||x2 ||x6|的最小值是 ；

    (3) 已知| x -1||x2 ||y-3||y4|10 求2xy 的最大值和最小值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】尺规作图是指用无刻度的直尺和圆规作图。尺规作图是起源于古希腊的数学课题.只使用圆规和直尺，并且只准许使用有限次，来解决不同的平面几何作图题.初中阶段同学们首次接触的尺规作图是“作一条线段等于已知线段”.

    图1

    图2

    备用图

    （1）如图1，在线段外有一点，现在利用尺规作图验证“两点之间线段最短”，.请根据提示，用尺规完成作图，并补充验证步骤.

    第一步，以为圆心，为半径作弧，交线段于点，则_____________；

    第二步，以为圆心，为半径作弧，交线段于点，则_____________；

    则____________________________________________

    故：.

    （2）如图2，在直线上，从左往右依次有四个点，，，，且，.现以为圆心，半径长为作圆，与直线两个交点中右侧交点记为点.再以为圆心；相同半径长作圆，与直线两个交点中左侧交点记为点.若，，三点中，有一点分另外两点所连线段之比为，求半径的长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，有一个边长为的大正方形和两个边长为b的小正方形，分别将他们按照图①和图②的形式摆放，

    （1）用含有的代数式分别表示阴影面积： , ， .

    （2）若，求的值；

    （3）若，，，求出图③中的阴影部分面积.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在边长为2的正方形ABCD中，P为AB的中点，Q为边CD上一动点，设DQ=t（0≤t≤2），线段PQ的垂直平分线分别交边AD、BC于点M、N，过Q作QE⊥AB于点E，过M作MF⊥BC于点F．

    （1）当t≠1时，求证：△PEQ≌△NFM；

    （2）顺次连接P、M、Q、N，设四边形PMQN的面积为S，求出S与自变量t之间的函数关系式，并求S的最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

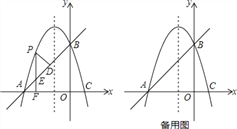
    【题目】如图，在平面直角坐标系xoy中,抛物线与轴交于点A（-3，0），C（1，0），与轴交于点B.

    （1）求此抛物线的解析式；

    （2）点P是直线AB上方的抛物线上一动点（不与点A,B重合），过点P作轴的垂线，垂足交点为F，交直线AB于点E，作于点D.

    ①点P在什么位置时，△PDE的周长最大，求出此时P点的坐标；

    ②连接PA，以PA为边作正方形APMN，当顶点M或N恰好落在抛物线对称轴上时，求出对应的P点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】李叔叔在“中央山水”买了一套经济适用房，他准备将地面铺上地砖，这套住宅的建筑平面（由四个长方形组成）如图所示（图中长度单位：米），请解答下问题：

    （1）用式子表示这所住宅的总面积；

    （2）若铺1平方米地砖平均费用120元，求当x=6时，这套住宅铺地砖总费用为多少元？

    查看答案和解析>>

    同步练习册答案