
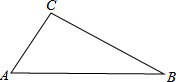
 如图,在Rt△ABC中,∠C=90°,AC=4,cosA=
如图,在Rt△ABC中,∠C=90°,AC=4,cosA=| 8 |
| 17 |
| 8 |
| 17 |
| AC |
| AB |
| 8 |
| 17 |
| 17 |
| 2 |
| AB2-AC2 |
| 15 |
| 2 |
| 15 |
| 2 |
| AC |
| BC |
| 4 | ||
|
| 8 |
| 15 |


 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:初中数学 来源: 题型:
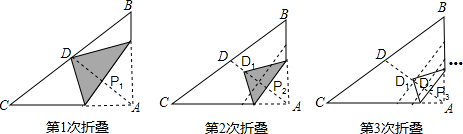
查看答案和解析>>
科目:初中数学 来源: 题型:
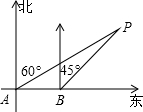 如图,海上有一灯塔P,在它周围15海里处有暗礁,一艘客轮以18海里/时的速度由西向东航行,行至A点处测得P在它的北偏东60°的方向,继续行驶40分钟后,到达B处又测得灯塔P在它的北偏东45°方向,问客轮不改变方向继续前进有无触礁的危险?(参考数据
如图,海上有一灯塔P,在它周围15海里处有暗礁,一艘客轮以18海里/时的速度由西向东航行,行至A点处测得P在它的北偏东60°的方向,继续行驶40分钟后,到达B处又测得灯塔P在它的北偏东45°方向,问客轮不改变方向继续前进有无触礁的危险?(参考数据| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
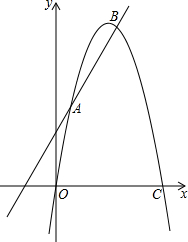 如图所示,已知抛物线y=ax2+bx+c与直线y=kx+4相交于A(1,5),B(4,8)两点,与x轴交于原点O及C点.
如图所示,已知抛物线y=ax2+bx+c与直线y=kx+4相交于A(1,5),B(4,8)两点,与x轴交于原点O及C点.| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、①②③ | B、②③④ |
| C、①②④ | D、①③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:
| x |
| 3 |
A、y=
| ||||
B、y=
| ||||
C、y=
| ||||
D、y=
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com