
| A. | DE:BC=AD:BD | B. | DE:BC=AB:AD | C. | AD:AE=AC:AB | D. | DB:EC=AB:AC |
分析 根据如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边,则当$\frac{AD}{AB}$=$\frac{AE}{AC}$或$\frac{AD}{DB}$=$\frac{AE}{EC}$时,DE∥BC,利用比例性质可判断D正确.
解答  解:如图,
解:如图,
当$\frac{AD}{AB}$=$\frac{AE}{AC}$或$\frac{AD}{DB}$=$\frac{AE}{EC}$时,DE∥BC.
所以$\frac{DB}{EC}$=$\frac{AB}{AC}$时,DE∥BC.
故选D.
点评 本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例;如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边.也考查了比例的性质.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | y1>y2 | B. | y1<y2 | C. | y1=y2 | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
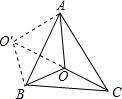 如图,等边△ABC内有一点O,且OA=10,OB=6,OC=8,求∠BOC的度数.(提示:将△AOC顺时针旋转60°后,AC与AB重合,连接OO′)
如图,等边△ABC内有一点O,且OA=10,OB=6,OC=8,求∠BOC的度数.(提示:将△AOC顺时针旋转60°后,AC与AB重合,连接OO′)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
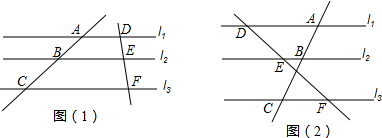
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com