
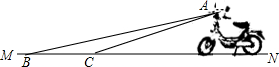
 齐河路路通电动车厂新开发的一种电动车如图,它的大灯A射出的光线AB,AC 与地面MN 所夹的锐角分别为8°和10°,大灯A与地面的距离为1m则该车大灯照亮地面的宽度BC是1.4m.(不考虑其它因素)
齐河路路通电动车厂新开发的一种电动车如图,它的大灯A射出的光线AB,AC 与地面MN 所夹的锐角分别为8°和10°,大灯A与地面的距离为1m则该车大灯照亮地面的宽度BC是1.4m.(不考虑其它因素)分析 根据题意作出合适的辅助线,可以分别求得BD、CD的长,从而可以求得BC的长,本题得以解决.
解答 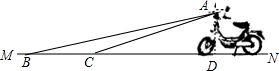 解:作AD⊥MN于点D,如右图所示,
解:作AD⊥MN于点D,如右图所示,
由题意可得,
AD=1m,∠ABD=8°,∠ACD=10°,∠ADC=∠ADB=90°,
∴BD=$\frac{AD}{tan8°}=\frac{1}{\frac{1}{7}}=7m$,
CD=$\frac{AD}{tan10°}=\frac{1}{\frac{5}{28}}=\frac{28}{5}=5.6$m,
∴BC=BD-CD=7-5.6=1.4m,
故答案为:1.4.
点评 本题考查解直角三角形的应用,解题的关键是明确题意,找出所求问题需要的条件.


科目:初中数学 来源: 题型:填空题
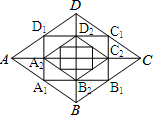 如图,菱形ABCD的对角线长分别为a、b,以菱形ABCD各边的中点为顶点作矩形A1B1C1D1,然后再以矩形A1B1C1D1的中点为顶点作菱形A2B2C2D2,…,如此下去,得到四边形A2016B2016C2016D2016的面积用含a,b的代数式表示为($\frac{1}{2}$)2017ab.
如图,菱形ABCD的对角线长分别为a、b,以菱形ABCD各边的中点为顶点作矩形A1B1C1D1,然后再以矩形A1B1C1D1的中点为顶点作菱形A2B2C2D2,…,如此下去,得到四边形A2016B2016C2016D2016的面积用含a,b的代数式表示为($\frac{1}{2}$)2017ab.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明同学起床后,来到院中呼吸一下新鲜空气,突然发现前几天栽好的一颗小树被昨晚的大风刮歪了(如图),小明正想把小树扶正时,突然想起,能否用学过的数学知识求出小树的主根与地面的夹角?能否求出小树被刮歪了多少度?请你帮小明想一想.
小明同学起床后,来到院中呼吸一下新鲜空气,突然发现前几天栽好的一颗小树被昨晚的大风刮歪了(如图),小明正想把小树扶正时,突然想起,能否用学过的数学知识求出小树的主根与地面的夹角?能否求出小树被刮歪了多少度?请你帮小明想一想.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | [(x-y)+5][(x+y)+5] | B. | [(x-y)+5][(x-y)-5] | C. | [(x+5)-y][(x+5)+y] | D. | [x-(y+5)][x+(y+5)] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com