
在图中,OA、BA分别表示甲、乙两人的运动图像,请根据图像回答下列问题:
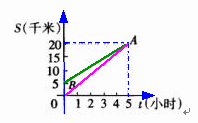
(1)求甲、乙的运动速度;
(2)甲和乙在出发前相距多远?
(3)两人同时出发,相遇时甲比乙多走了多少米?
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
 点B开始在线段BA上以每秒2个单位长度的速度向点A运动,设点P、Q运动的时间为t秒.
点B开始在线段BA上以每秒2个单位长度的速度向点A运动,设点P、Q运动的时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:
 A上,BD=BA,点Q是线段BD上一个动点,点P的坐标是(0,3),设直线PQ的解析式为y=kx+b.
A上,BD=BA,点Q是线段BD上一个动点,点P的坐标是(0,3),设直线PQ的解析式为y=kx+b.查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,直角梯形OABC的顶点A、B的坐标分别是![]() 、
、![]() ,点D在线段OA上,BD=BA, 点Q是线段BD上一个动点,点P的坐标是
,点D在线段OA上,BD=BA, 点Q是线段BD上一个动点,点P的坐标是![]() ,设直线PQ的解析式为
,设直线PQ的解析式为![]() .
.
(1)求k的取值范围;
(2)当k为取值范围内的最大整数时,若抛物线![]() 的顶点在直线PQ、OA、AB、BC围成的四边形内部,求a的取值范围.
的顶点在直线PQ、OA、AB、BC围成的四边形内部,求a的取值范围.

查看答案和解析>>
科目:初中数学 来源:2011-2012学年江苏泰兴市实验中学八年级上学期期末考试数学试卷(带解析) 题型:解答题
如图,矩形OABC的边OA在x轴正半轴上,边OC在y轴正半轴上,B点的坐标为(1,3).矩形O'A'BC'是矩形OABC绕B点逆时针旋转得到的.O'点恰好在x轴的正半轴上, O'C'交AB于点D.
(1)求点O'的坐标,并判断△O'DB的形状(要说明理由)(4分)
(2)求边C'O'所在直线的解析式.(4分)
(3)延长BA到M使AM=1,在(2)中求得的直线上是否存在点P,使得ΔPOM是以线段OM为直角边的直角三角形?若存在,请直接写出P点的坐标;若不存在,请说明理由.(2分)
查看答案和解析>>
科目:初中数学 来源:2013届江苏泰兴市八年级上学期期末考试数学试卷(解析版) 题型:解答题
如图,矩形OABC的边OA在x轴正半轴上,边OC在y轴正半轴上,B点的坐标为(1,3).矩形O'A'BC'是矩形OABC绕B点逆时针旋转得到的.O'点恰好在x轴的正半轴上, O'C'交AB于点D.

(1)求点O'的坐标,并判断△O'DB的形状(要说明理由)(4分)
(2)求边C'O'所在直线的解析式.(4分)
(3)延长BA到M使AM=1,在(2)中求得的直线上是否存在点P,使得ΔPOM是以线段OM为直角边的直角三角形?若存在,请直接写出P点的坐标;若不存在,请说明理由.(2分)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com