
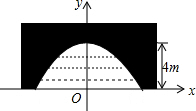
 如图是一座古拱桥的截面图,拱桥洞是抛物线形状,其跨度为10m,桥洞与水面的最大距离为4m,将拱桥的横截面放在如图所示的平面直角坐标系中.
如图是一座古拱桥的截面图,拱桥洞是抛物线形状,其跨度为10m,桥洞与水面的最大距离为4m,将拱桥的横截面放在如图所示的平面直角坐标系中.分析 (1)由图象可知抛物线的顶点坐标(0,4),设这条抛物线所对应的函数关系式为y=ax2+4,经过(5,0),求得a;
(2)把y=3代入即可解决.
解答 解:(1)由题意得:抛物线的顶点坐标为(0,4),设这条抛物线所对应的函数关系式为y=ax2+4,
∵图象经过(5,0),
∴0=25a+4,
解得a=-$\frac{4}{25}$,
∴抛物线的解析式为y=-$\frac{4}{25}$x2+4;
(2)把y=3代入y=-$\frac{4}{25}$x2+4,得
3=-$\frac{4}{25}$x2+4,
解得:x=±2.5,
∴两盏景观灯间的水平距离为5米.
点评 本题主要考查二次函数的应用,本题运用二次函数的顶点坐标式,运用二次函数解决实际问题,比较简单.


科目:初中数学 来源: 题型:解答题
 已知,如图,四边形ABCD是平行四边形,E是AB延长线上一点,DE交对角线AC于G.
已知,如图,四边形ABCD是平行四边形,E是AB延长线上一点,DE交对角线AC于G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某数学兴趣小组的同学再一次探究中发现:若平面直角坐标系中有两点A(x1,y1)和B(x2,y2),则线段AB的中点C的坐标为($\frac{{{x_1}+{x_2}}}{2},\frac{{{y_1}+{y_2}}}{2}$).经过进一步的讨论,他们呢借助中位线和一次函数的知识证明了这一结论,请你使用该结论解答下面问题.
某数学兴趣小组的同学再一次探究中发现:若平面直角坐标系中有两点A(x1,y1)和B(x2,y2),则线段AB的中点C的坐标为($\frac{{{x_1}+{x_2}}}{2},\frac{{{y_1}+{y_2}}}{2}$).经过进一步的讨论,他们呢借助中位线和一次函数的知识证明了这一结论,请你使用该结论解答下面问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
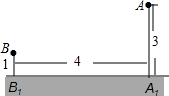 如图,大江的一侧有A、B两个工厂,它们有垂直于江边的小路,长度分别为3千米和1千米,设两条小路相距4千米,现在要在江边建立一个抽水站,把水送到A、B两厂去,欲使供水管路最短,抽水站应建在哪里?
如图,大江的一侧有A、B两个工厂,它们有垂直于江边的小路,长度分别为3千米和1千米,设两条小路相距4千米,现在要在江边建立一个抽水站,把水送到A、B两厂去,欲使供水管路最短,抽水站应建在哪里?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图.
已知:如图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com