练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    9．在△ABC中，∠ABC=∠ACB，BD是AC边上的高，且∠ABD=15°，求∠ACB的度数．

    分析 根据三角形的内角和即可得到结论．

    解答 解：如图1，
    ∵BD是AC边上的高，且∠ABD=15°，
    ∴∠A=75°，
    ∴∠ABC=∠ACB=52.5°，
    如图2，∵BD是AC边上的高，且∠ABD=15°，
    ∴∠DAB=75°，
    ∴∠ABC=∠ACB=$\frac{1}{2}$∠DAB=37.5°，
    ∴∠ACB的度数是52.5°或37.5°．

    点评 本题考查了三角形的内角和，正确的作出图形是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    1．某种正方形合金板材的成本y（元）与它的面积成正比．设它的边长为x厘米，当x=2时，y=16，那么当成本为72元时，边长为（　　）
    A．4厘米B．3$\sqrt{2}$厘米C．2$\sqrt{3}$厘米D．6厘米

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

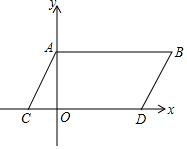    1．如图，在平面直角坐标系中，点A，B坐标分别为A（0，a），B（b，a），且实数a，b满足（a-3）2+|b-5|=0，现同时将点A，B分别向下平移3个单位，再向左平移1个单位，分别得到点A，B的对应点C，D，连接AC，BD，AB．
    （1）求点C，D的坐标及四边形ABDC的面积；
    （2）在y轴上是否存在一点M，连接MC，MD，使S△MCD=S四边形ABDC？若存在这样一点，求出点M的坐标；若不存在，试说明理由．

    查看答案和解析>>

    科目：初中数学 来源：2017届湖北省枝江市九年级3月调研考试数学试卷（解析版） 题型：判断题

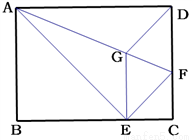
    如图，将矩形ABCD沿AF折叠，使点D落在BC边的点E处，过点E作EG∥CD交AF于点G，连接DG．

    (1)求证：四边形EFDG是菱形；

    (2)探究线段EG，GF，AF之间的数量关系，并说明理由；

    (3)若AG=6，EG=2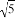，求BE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．下面是“经过已知直线外一点作这条直线的平行线”的尺规作图过程．
    已知：如图1，直线l和直线l外一点P．
    求作：直线l的平行直线，使它经过点P．
    作法：如图2．
    （1）过点P作直线m与直线l交于点O；
    （2）在直线m上取一点A（OA＜OP），以点O为圆心，OA长为半径画弧，与直线l交于点B；
    （3）以点P为圆心，OA长为半径画弧，交直线m于点C，以点C为圆心，AB长为半径画弧，两弧交于点D；
    （4）作直线PD．
    所以直线PD就是所求作的平行线．
    请回答：该作图的依据是三边分别相等的两个三角形全等；全等三角形的对应角相等；同位角相等，两直线平行．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    14．化简：$\frac{{x}^{2}+3x}{x}$=x+3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．问题再现：
    数形结合是解决数学问题的一种重要的思想方法，借助这种方法可将抽象的数学知识变得直观起来并且具有可操作性，从而可以帮助我们快速解题．初中数学里的一些代数公式，很多都可以通过表示几何图形面积的方法进行直观推导和解释．
    例如：利用图形的几何意义证明完全平方公式．
    证明：将一个边长为a的正方形的边长增加b，形成两个矩形和两个正方形，如图1：
    这个图形的面积可以表示成：
    （a+b）2或　a2+2ab+b2
    ∴（a+b）2 =a2+2ab+b2
    这就验证了两数和的完全平方公式．
    类比解决：
    （1）请你类比上述方法，利用图形的几何意义证明平方差公式．（要求画出图形并写出推理过程）
    问题提出：如何利用图形几何意义的方法证明：13+23=32？
    如图2，A表示1个1×1的正方形，即：1×1×1=13
    B表示1个2×2的正方形，C与D恰好可以拼成1个2×2的正方形，因此：B、C、D就可以表示2个2×2的正方形，即：2×2×2=23
    而A、B、C、D恰好可以拼成一个（1+2）×（1+2）的大正方形．
    由此可得：13+23=（1+2）2=32
    尝试解决：
    （2）请你类比上述推导过程，利用图形的几何意义确定：13+23+33=62．（要求写出结论并构造图形写出推证过程）．
    （3）问题拓广：
    请用上面的表示几何图形面积的方法探究：13+23+33+…+n3=[$\frac{1}{2}$n（n+1）]2．（直接写出结论即可，不必写出解题过程）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．解方程组：
    （1）$\left\{\begin{array}{l}2x=y+3\\ 3x+2y=8.\end{array}\right.$        
    （2）$\left\{\begin{array}{l}3x=5y-9\\ y-x=3.\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．已知二次函数y=ax2+bx+c中，函数y与自变量x的部分对应值如下表：
    x…-10123…
    y…105212…
    （1）求该函数的表达式；
    （2）当y＜5时，x的取值范围是0＜x＜4．

    查看答案和解析>>

    同步练习册答案