
【题目】王老师将1个黑球和若干个白球放入一个不透明的口袋并搅匀,让若干学生进行摸球实验,每次摸出一个球(有放回),下表是活动进行中的一组统计数据.
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到黑球的次数m | 23 | 31 | 60 | 130 | 203 | 251 |
摸到黑球的频率 | 0.23 | 0.21 | 0.30 | 0.26 | 0.253 |
(1)补全上表中的有关数据,根据上表数据估计从袋中摸出一个球是黑球的概率是 ;(精确到0.01)
(2)估算袋中白球的个数.
科目:初中数学 来源: 题型:
【题目】我们经历了“确定函数的表达式﹣利用函数图象研究其性质﹣运用函数解决问题”的学习过程在画函数图象时,我们通过描点的方法画出了所学的函数图象同时,我们也学习了绝对值的意义:|a|=![]() ,结合上面经历的学习过程,解决下面问题:
,结合上面经历的学习过程,解决下面问题:
(1)若一次函数y=kx+b的图象分别经过点A(﹣1,1),B(2,2),请求出此函数表达式;
(2)在给出的平面直角坐标系中,直接画出函数y=|x|和y=kx+b的图象;
(3)根据这两个函数图象直接写出不等式|x|≤kx+b的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD,对角线的交点M(2,2).规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换.如此这样,连续经过2014次变换后,正方形ABCD的对角线交点M的坐标变为( )
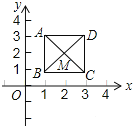
A. (﹣2012,2)B. (﹣2012,﹣2)C. (﹣2013,﹣2)D. (﹣2013,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图△ABC中,BC=3,以BC为直径的⊙O交AC于点D,若D是AC中点,∠ABC=120°.
(1)求∠ACB的大小;
(2)求点A到直线BC的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F,连接CF.
(1)求证:AF=BD.
(2)求证:四边形ADCF是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,连接CD,过E作EF∥DC交BC的延长线于F.
(1)证明:四边形CDEF是平行四边形;
(2)若四边形CDEF的周长是16cm,AC的长为8cm,求线段AB的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() 点是第二象限内一点,
点是第二象限内一点,![]() 轴于
轴于![]() ,且
,且![]() 是
是![]() 轴正半轴上一点,
轴正半轴上一点,![]() 是x轴负半
是x轴负半![]() 轴上一点,且
轴上一点,且![]() .
.

(1)![]() ( ),
( ),![]() ( )
( )
(2)如图2,设![]() 为线段
为线段![]() 上一动点,当
上一动点,当![]() 时,
时,![]() 的角平分线与
的角平分线与![]() 的角平分线的反向延长线交于点
的角平分线的反向延长线交于点![]() ,求
,求![]() 的度数: (注: 三角形三个内角的和为
的度数: (注: 三角形三个内角的和为![]() )
)
(3)如图3,当![]() 点在线段
点在线段![]() 上运动时,作
上运动时,作![]() 交
交![]() 于
于![]() 的平分线交于
的平分线交于![]() ,当
,当![]() 点在运动的过程中,
点在运动的过程中,![]() 的大小是否变化?若不变,求出其值;若变化,请说明理由.
的大小是否变化?若不变,求出其值;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请完成下列的相似测试.
如图,在△ABC中,AB=AC=4,D是AB上一点,且BD=1,连接CD,然后作∠CDE=∠B,交平行于BC且过点A的直线于点E,DE交AC于点F,连接CE.
(1)求证:△AFD∽△EFC;
(2)试求AEBC的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com