
分析 根据cotα=$\frac{cosα}{sinα}$,cos2α+sin2α=1,可得答案.
解答 解:由题意,得
cosα=2sinα.
$\frac{sinα•cosα}{1-sinα•cosα}$=$\frac{2si{n}^{2}α}{co{s}^{2}α+si{n}^{2}α-2si{n}^{2}α}$
=$\frac{2si{n}^{2}α}{co{s}^{2}α-si{n}^{2}α}$
=$\frac{2}{co{t}^{2}α-1}$
=$\frac{2}{{2}^{2}-1}$
=$\frac{2}{3}$.
点评 本题考查了同角三角函数关系,利用cotα=$\frac{cosα}{sinα}$,cos2α+sin2α=1是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
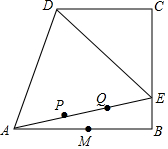 如图四边形ABCD,∠B=∠C=90°,AB=BC=4,△AED为等边三角形,M为AB中点,E为BC上一点,动点P,Q同时从A出发向点E运动,P的速度为1单位/秒,Q的速度为2单位/秒,当Q到达E时,两点同时停止运动,设t秒后,PQ+QM的值最小,求此最小值和t.
如图四边形ABCD,∠B=∠C=90°,AB=BC=4,△AED为等边三角形,M为AB中点,E为BC上一点,动点P,Q同时从A出发向点E运动,P的速度为1单位/秒,Q的速度为2单位/秒,当Q到达E时,两点同时停止运动,设t秒后,PQ+QM的值最小,求此最小值和t.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com