

分析 (1)根据题意可以求得任意转动转盘一次,获得猴年邮票的概率;
(2)根据题意可以写出转动转盘两次,所有可能出现的结果,然后找出符合要求的可能结果,即可求得相应的概率.
解答 解:(1)由题意可得,
任意转动转盘一次,获得猴年邮票的概率是$\frac{1}{4}$,
故答案为:$\frac{1}{4}$;
(2)∵转动转盘两次,所有可能出现的结果有:(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4),共有16种,它们出现的可能性相同,
∴所有的结果中,满足“转动转盘两次,获得的两枚邮票可以邮寄一封需2.4元邮资的信件”(记为事件A)的结果有9种,所以P(A)=$\frac{9}{16}$,
即任意转动转盘两次,获得的两枚邮票可以邮寄一封需2.4元邮资的信件的概率是$\frac{9}{16}$.
点评 本题考查列表法与树状图法,解题的关键是明确题意,可以算出相应事件发生的可能性和发生的所有可能性,会计算相应的事件的概率.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
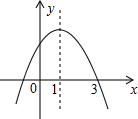 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,现有下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,现有下列结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.511×109 | B. | 5.11×108 | C. | 51.1×107 | D. | 511×106 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,AB=AC=5,BC=6,将△ABC绕点B逆时针旋转60°得到△A′BC′,连接A′C,则A′C的长为4+3$\sqrt{3}$.
如图,在△ABC中,AB=AC=5,BC=6,将△ABC绕点B逆时针旋转60°得到△A′BC′,连接A′C,则A′C的长为4+3$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC和△DCB中,AB=DC,AC=DB,AC与DB交于点M.
如图,在△ABC和△DCB中,AB=DC,AC=DB,AC与DB交于点M.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com