练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20．如图，是由4个完全相同的小正方体组成的立体图形，它的主视图是（　　）
    A．B．C．D．

    分析 根据从正面看得到的图形是主视图，可得答案．

    解答 解：从正面看第一层是三个小正方形，第二层中间一个小正方形，
    故选：C．

    点评 本题考查了简单组合体的三视图，从正面看得到的图形是主视图．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

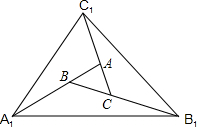    10．如图，对面积为1的△ABC逐次进行以下操作：第一次操作，分别延长AB、BC、CA至点A1、B1、C1，使得A1B=AB，B1C=BC，C1A=CA，顺次连接A1、B1、C1，得到△A1B1C1，记其面积为S1；第二次操作，分别延长A1B1，B1C1，C1A1至A2，B2，C2，使得A2B1=A1B1，B2C1=B1C1，C2A1=C1A1，顺次连接A2，B2，C2，得到△A2B2C2，记其面积为S2…，按此规律继续下去．第n次操作得到△AnBnCn，则S1=7，△AnBnCn的面积Sn=7n．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．正方形A1B1C1O，A2B2C2C1，A3B3C3C2，…，按如图所示的方式放置．点A1，A2，A3，…，和点C1，C2，C3，…，分别在直线y=x+1和x轴上，则点B1的坐标是（1，1）；点Bn的坐标是${B_n}（{{2^n}-1，{2^{n-1}}}）$．（用含n的代数式表示）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．已知：如图，∠ACB=∠DBC，如果要说明△AOB≌△DOC，那么还需要添加一个条件，这个条件可以是∠A=∠D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．计算：
    （1）$\sqrt{2（6+\sqrt{3}）+（1-\sqrt{3}）^{2}}$；
    （2）（7${\;}^{\frac{3}{2}}$×49${\;}^{-\frac{3}{4}}$）${\;}^{\frac{1}{3}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．如图，已知△ABC是腰长为1的等腰直角三形，以Rt△ABC的斜边AC为直角边，画第二个等腰Rt△ACD，再以Rt△ACD的斜边AD为直角边，画第三个等腰Rt△ADE，…，依此类推，则第2015个等腰直角三角形的斜边长是（　　）
    A．${（{\sqrt{2}}）^{2014}}$B．${（{\sqrt{2}}）^{2015}}$C．22014D．22015

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．阅读下列材料，并用相关的思想方法解决问题．
    计算：（1-$\frac{1}{2}$-$\frac{1}{3}$-$\frac{1}{4}$）×（$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+$\frac{1}{5}$）-（1-$\frac{1}{2}$-$\frac{1}{3}$-$\frac{1}{4}$-$\frac{1}{5}$）×（$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$）．
    令$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$=t，则
    原式=（1-t）（t+$\frac{1}{5}$）-（1-t-$\frac{1}{5}$）t
    =t+$\frac{1}{5}$-t2-$\frac{1}{5}$t-$\frac{4}{5}$t+t2
    =$\frac{1}{5}$
    问题：
    （1）计算
    （1-$\frac{1}{2}$-$\frac{1}{3}$-$\frac{1}{4}$-…-$\frac{1}{2014}$）×（$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+$\frac{1}{5}$+…+$\frac{1}{2014}$+$\frac{1}{2015}$）-（1-$\frac{1}{2}$-$\frac{1}{3}$-$\frac{1}{4}$-$\frac{1}{5}$-…-$\frac{1}{2014}$-$\frac{1}{2015}$）×（$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+…+$\frac{1}{2014}$）；
    （2）解方程（x2+5x+1）（x2+5x+7）=7．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．已知二次函数y=x2+mx+n的图象经过点P（-3，1），对称轴是经过（-1，0）且平行于y轴的直线．
    （1）求m、n的值；
    （2）如图，一次函数y=kx+b的图象经过点P，与x轴相交于点A，与二次函数的图象相交于另一点B，点B在点P的右侧，PA：PB=1：5，求一次函数的表达式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．下列命题正确的是（　　）
    A．对角线互相垂直的四边形是菱形
    B．一组对边相等，另一组对边平行的四边形是平行四边形
    C．对角线相等的四边形是矩形
    D．对角线互相垂直平分且相等的四边形是正方形

    查看答案和解析>>

    同步练习册答案