
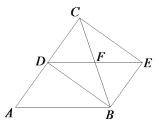
【题目】如图,已知ABED,延长AD到C使AD=DC,连接BC,CE,BC交DE于点F,若AB=BC.
(1)求证:四边形BECD是矩形;
(2)连接AE,若∠BAC=60°,AB=4,求AE的长.
【答案】(1)见解析;(2) ![]()
【解析】
(1)根据平行四边形的性质得到AD=BE,由此推出四边形BECD是平行四边形,由AB=BC根据等腰三角形的性质得到BD⊥AC,即可推出结论;
(2)根据AB=BC,∠BAC=60°,推出△ABC是等边三角形,得到AC=AB=4,利用四边形BECD是矩形,求出∠ADB=∠DCE=90°,利用三角函数求出CE=BD=![]() ,再利用勾股定理求出AE.
,再利用勾股定理求出AE.
(1)∵四边形ABED是平行四边形,
∴AD=BE,AC∥BE,
∵AD=DC,
∴BE=DC,
∴四边形BECD是平行四边形,
∵AB=BC,
∴BD⊥AC,
∴∠BDC=90°,
∴四边形BECD是矩形;
(2)∵AB=BC,∠BAC=60°,
∴△ABC是等边三角形,
∴AC=AB=4,
∵四边形BECD是矩形,
∴∠ADB=∠DCE=90°,
∴CE=BD=![]() ,
,
∴AE=![]() .
.



 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC各顶点的坐标分别为A(-2,6),B(-3,2),C(0,3),将△ABC先向右平移4个单位长度,再向上平移3个单位长度,得到△DEF.
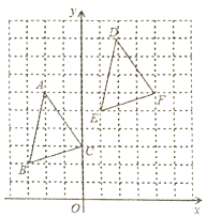
(1)分别写出△DEF各顶点的坐标;
(2)如果将△DEF看成是由△ABC经过一次平移得到的,请指出这一平移的平移方向和平移距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,锐角△ABC中,D,E分别是AB,AC边上的点,△ADC≌![]() ,△AEB≌
,△AEB≌![]() ,且
,且![]() ,BE、CD交于点F,若∠BAC=40°,则∠BFC的大小是( )
,BE、CD交于点F,若∠BAC=40°,则∠BFC的大小是( )

A.105°B.100°C.110°D.115°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题14分)如图(1),在△ABC和△EDC中,D为△ABC边AC上一点,CA平分∠BCE,BC=CD,AC=CE.


(1)求证:△ABC≌△EDC;
(2)如图(2),若∠ACB=60°,连接BE交AC于F,G为边CE上一点,满足CG=CF,连接DG交BE于H.
①求∠DHF的度数;
②若EB平分∠DEC,试说明:BE平分∠ABC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是

A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=2x﹣6与反比例函数![]() 的图象交于点A(4,2),与x轴交于点B.
的图象交于点A(4,2),与x轴交于点B.
(1)求k的值及点B的坐标;
(2)在x轴上是否存在点C,使得AC=AB?若存在,求出点C的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工厂接到订单,需要边长为(a+3)和3的两种正方形卡纸.
(1)仓库只有边长为(a+3)的正方形卡纸,现决定将部分边长为(a+3)的正方形纸片,按图甲所示裁剪得边长为3的正方形.

①如图乙,求裁剪正方形后剩余部分的面积(用含a代数式来表示);
②剩余部分沿虚线又剪拼成一个如图丙所示长方形(不重叠无缝隙),则拼成的长方形的边长多少?(用含a代数式来表示);
(2)若将裁得正方形与原有正方形卡纸放入长方体盒子底部,按图1,图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),盒子底部中未被这两张正方形纸片覆盖的部分用阴影表示,设图1中阴影部分的面积为S1,图2中阴影部分的面积为S2测得盒子底部长方形长比宽多3,则S2﹣S1的值为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售一款口罩,每袋的进价为12元,计划售价大于12元但不超过22元,通过试场调查发现,这种口罩每袋售价提高1元,日均销售量降低5袋,当售价为18元时,日均销售量为50袋.
(1)在售价为18元的基础上,将这种口罩的售价每袋提高x元,则日均销售量是 袋;(用含x的代数式表示)
(2)要想销售这种口罩每天赢利275元,该商场每袋口罩的售价要定为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com