
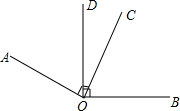
 如图,若AO⊥OC,BO⊥DO,
如图,若AO⊥OC,BO⊥DO,分析 (1)根据垂直的定义、结合图形计算即可;
(2)根据直角相等、同角的余角相等解答;
(3)设∠DOC=x,根据题意列出方程,解方程即可;
(4)设∠AOD=∠DOC=∠COB=x,结合图形列出方程,解方程即可
解答 解:(1)∵AO⊥OC,BO⊥DO,
∴∠AOC=∠BOD=90°,
∴∠AOB=2(90°一38°)+38°=142°;
(2)∠AOC=∠BOD=90°,∠AOD=∠BOC;
(3)设∠DOC=x,则2(90°一x)+x=156°
∴x=24°;
(4)能相等.
设∠AOD=∠DOC=∠COB=x.则
90°-x=x,
∴x=45°.
点评 本题考查的是垂线的概念、余角和补角的概念,掌握垂直的定义、余角和补角的概念是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
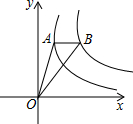 如图,点A是反比例函数y1=$\frac{1}{x}$(x>0)图象上一点,过点A作x轴的平行线,交反比例函数y2=$\frac{k}{x}$(x>0)的图象于点B,连接OA、OB,若△OAB的面积为2,则k的值为5.
如图,点A是反比例函数y1=$\frac{1}{x}$(x>0)图象上一点,过点A作x轴的平行线,交反比例函数y2=$\frac{k}{x}$(x>0)的图象于点B,连接OA、OB,若△OAB的面积为2,则k的值为5.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
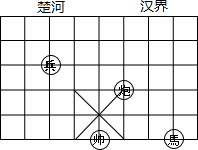 如图,若在象棋盘上建立直角坐标系,使“帥”位于点(-1,-2),“馬”位于点(2,-2),则“炮”位于点( )
如图,若在象棋盘上建立直角坐标系,使“帥”位于点(-1,-2),“馬”位于点(2,-2),则“炮”位于点( )| A. | (0,1 ) | B. | (0,-1) | C. | (0,0) | D. | (1,0) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
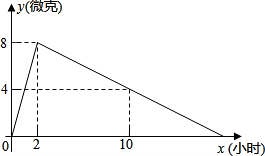 某医药研究所开发了一种新药,在试验药效时发现,如果成人按规定剂量服用,那么服药后2小时时血液中含药量最高,达每毫升8微克(1000微克=1毫克),接着逐步衰减,10小时时血液中含药量为每毫升4微克,每毫升血液中含药量y(微克),随时间x(小时)的变化如图所示.当成人按规定剂量服药后:
某医药研究所开发了一种新药,在试验药效时发现,如果成人按规定剂量服用,那么服药后2小时时血液中含药量最高,达每毫升8微克(1000微克=1毫克),接着逐步衰减,10小时时血液中含药量为每毫升4微克,每毫升血液中含药量y(微克),随时间x(小时)的变化如图所示.当成人按规定剂量服药后:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 在如图所示的平面直角坐标系中,一只蚂蚁从A点出发,沿着A-B-C-D-A…循环爬行,其中A点坐标为(1,-1),B的坐标为(-1,-1),C的坐标为(-1,3),D的坐标为(1,3),当蚂蚁爬了2015个单位时,它所处位置的坐标为(1,0).
在如图所示的平面直角坐标系中,一只蚂蚁从A点出发,沿着A-B-C-D-A…循环爬行,其中A点坐标为(1,-1),B的坐标为(-1,-1),C的坐标为(-1,3),D的坐标为(1,3),当蚂蚁爬了2015个单位时,它所处位置的坐标为(1,0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com