【题目】某校九年级（1）班50名学生需要参加体育“五选一”自选项目测试，班上学生所报自选项目的情况统计如表所示：
自选项目 | 人数 | 频率 |
立定跳远 | b | 0.18 |
三级蛙跳 | 12 | 0.24 |
一分钟跳绳 | 8 | a |
投掷实心球 | 16 | 0.32 |
推铅球 | 5 | 0.10 |
合计 | 50 | 1 |
（1）求a，b的值；
（2）若该校九年级共有400名学生，试估计年级选择“一分钟跳绳”项目的总人数；
（3）在选报“推铅球”的学生中，有3名男生，2名女生，为了了解学生的训练效果，从这5名学生中随机抽取两名学生进行推铅球测试，求所抽取的两名学生中至少有一名女生的概率．
【答案】（1）a＝0.16；b＝9；（2）64；（3）
．
【解析】
（1）根据表格求出a与b的值即可；
（2）计算出50名学生选择“一分钟跳绳”项目的人数，进而可估计该校九年级有400名学生，选择“一分钟跳绳”项目的总人数；
（3）列表得出所有等可能的情况数，找出抽取的两名学生中至少有一名女生的情况，即可求出所求概率．
解：（1）根据题意得：a＝1﹣（0.18+0.24+0.32+0.10）＝0.16；
b＝50×0.18＝9；
（2）
（人）；
（3）男生编号为A、B、C，女生编号为D、E，
男A | 男B | 男C | 女D | 女E | |
男A | （B，A） | （C，A） | （D，A） | （E，A） | |
男B | （A，B） | （C，B） | （D，B） | （E，B） | |
男C | （A，C） | （B，C） | （D，C） | （E，C） | |
女D | （A，D） | （B，D） | （C，D） | （E，D） | |
女E | （A，E） | （B，E） | （C，E） | （D，E） |
共有20种情况，其中有1名女生的情况有12种，有2名女生的情况有2种，因此至少有一名女生的情况包括两种情况，共14种，
∴抽取的两名学生中至少有一名女生的概率为：
=．
科目：初中数学 来源： 题型：
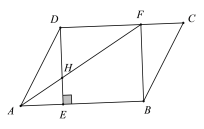
【题目】在平行四边形 ABCD 中，过点 D 作 DE⊥AB 于点 E，点 F 在 CD 上，CF =AE，连接 BF，AF．
（1）求证：四边形 BFDE 是矩形；
（2）若 AF 平分∠BAD，交DE与H点，且 AB=3AE，BF=6，求AH的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
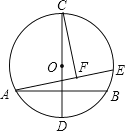
【题目】如图，在半径为4的⊙O中，CD为直径，AB⊥CD且过半径OD的中点，点E为⊙O上一动点，CF⊥AE于点F.当点E从点B出发顺时针运动到点D时，点F所经过的路径长为( )
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】学以致用：问题1：怎样用长为
的铁丝围成一个面积最大的矩形？
小学时我们就知道结论：围成正方形时面积最大，即围成边长为
的正方形时面积最大为
．请用你所学的二次函数的知识解释原因．
思考验证：问题2：怎样用铁丝围一个面积为
且周长最小的矩形？
小明猜测：围成正方形时周长最小．
为了说明其中的道理，小明翻阅书籍，找到下面的结论：
在
、
均为正实数）中，若
为定值
，则
，只有当
时，
有最小值
．
思考验证：证明：
、均为正实数）
请完成小明的证明过程：
证明：对于任意正实数
、
解决问题：
（1）若
，则
（当且仅当
时取“
” 
；
（2）运用上述结论证明小明对问题2的猜测；
（3）填空：当
时，
的最小值为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了发展乡村旅游，建设美丽乡村，某中学七年级（1）班同学都积极参加了植树活动，将今年三月份该班同学的植树情况绘制成如图所示的不完整的统计图．已知植树量为2株的人数占总人数的32%．
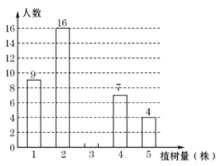
（1）该班的总人数为____________，植树株数的众数是____________，植树株数的中位数是____________；
（2）请将条形统计图补充完整；
（3）若将该班同学的植树情况绘制成扇形统计图，求“植树量为3株”所对应的扇形的园心角度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
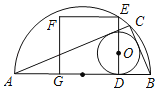
【题目】如图，AB为半圆的直径，C是半圆弧上一点，正方形DEFG的一边DG在直径AB上，另一边DE过△ABC的内切圆圆心O，且点E在半圆上．
（1）当正方形的顶点F也在半圆弧上时，半圆的半径与正方形边长的比为 ；
（2）当正方形DEFG的面积为100，且△ABC的内切圆⊙O的半径r＝4，求半圆的直径AB的值；
（3）若半圆的半径为R，直接写出⊙O半径r可取得的最大值．
查看答案和解析>>
科目：初中数学 来源： 题型：
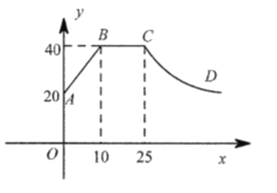
【题目】一般情况下，学生注意力上课后逐渐增强，中间有段时间处于较理想的稳定状态，随后开始分散．实验结果表明，学生注意力指数y随时间x(min)的变化规律如图所示(其中
分别为线段，
为双曲线的一部分)：
（1）上课后第
与第
相比较，何时学生注意力更集中？
（2）某道难题需连续讲
，为保证效果，学生注意力指数不宜低于
，老师能否在所需要求下讲完这道题？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图（1），已知点G在正方形ABCD的对角线AC上，GE⊥BC，垂足为点E，GF⊥CD，垂足为点F．
（1）证明与推断：
①求证：四边形CEGF是正方形；
②推断：
的值为 ：
（2）探究与证明：
将正方形CEGF绕点C顺时针方向旋转α角（0°＜α＜45°），如图（2）所示，试探究线段AG与BE之间的数量关系，并说明理由：
（3）拓展与运用：
正方形CEGF在旋转过程中，当B，E，F三点在一条直线上时，如图（3）所示，延长CG交AD于点H．若AG=6，GH=2
，则BC= ．
查看答案和解析>>
科目：初中数学 来源： 题型：
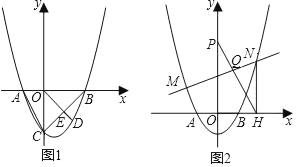
【题目】如图1，抛物线y＝x2+（m﹣2）x﹣2m（m＞0）与x轴交于A、B两点（A在B左边），与y轴交于点C．连接AC、BC，D为抛物线上一动点（D在B、C两点之间），OD交BC于E点．
（1）若△ABC的面积为8，求m的值；
（2）在（1）的条件下，求
的最大值；
（3）如图2，直线y＝kx+b与抛物线交于M、N两点（M不与A重合，M在N左边），连MA，作NH⊥x轴于H，过点H作HP∥MA交y轴于点P，PH交MN于点Q，求点Q的横坐标．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com