
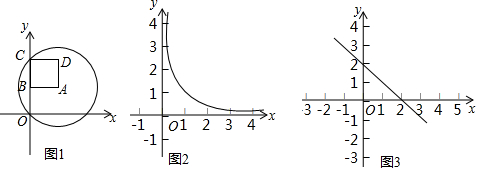
���� ��1����ͼ1�У�����OA����Rt��AOB�У����ù��ɶ������OA���ɣ�
��2�������A�İ뾶�Լ�AC�ij��������жϣ���AC=OAʱ����C�ڡ�A�ϣ���AC��OAʱ����C�ڡ�A�⣬��AC��OAʱ����C�ڡ�A�ڣ�
��3���������֪��C��0��2��������AC��OA�����ɼ������⣬ע��m��0��
��� �⣺��1����ͼ1�У�����OA��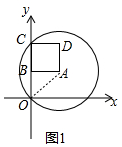
��A��1��1����AB��y�ᣬ
��AB=OB=1����ABO=90�㣬
��OA=$\sqrt{A{B}^{2}+O{B}^{2}}$=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$��
���A�İ뾶Ϊ$\sqrt{2}$��
�ʴ�Ϊ$\sqrt{2}$��
��2����ͼ2�У�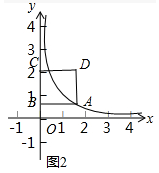
��A��2��$\frac{1}{2}$������O A=$\sqrt{4+\frac{1}{4}}=\frac{{\sqrt{17}}}{2}$
��AC=$2\sqrt{2}$=$\frac{{4\sqrt{2}}}{2}$=$\frac{{\sqrt{32}}}{2}$
��O A��A C��
���C�ڡ�A�⣮
������ͼ�����ù��ɶ���ֱ�۷�������OB��BC��AB=AB����O A��A CҲ���ԣ�
��3����ͼ3�У�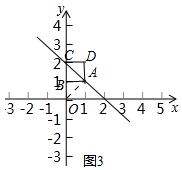
�ߵ�A��ֱ��y=-x+2��һ���㣬ֱ�����������Ǽн�Ϊ45�㣬
�֡��ı���ABCD�������Σ�
���C��0��2����
�൱AC��OAʱ��������ABCD�ڡ�A�ڲ���
��AC=OAʱ����A��1��1����
��m��1ʱ��AC��OA��
��m=0ʱ�������β����ڣ�
��m��1��m��0ʱ��������ABCD�ڡ�A�ڲ���
���� ���⿼��Բ�ۺ��⡢�����ε����ʡ����������������ʡ�һ�κ�����Ӧ�õ�֪ʶ������Ĺؼ����������⣬���յ�AC=OAʱ����C�ڡ�A�ϣ���AC��OAʱ����C�ڡ�A�⣬��AC��OAʱ����C�ڡ�A�ڣ������п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 45�� | B�� | 60�� | C�� | 30�� | D�� | 90�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �ȱ������� | B�� | �������� | C�� | ���� | D�� | ����� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
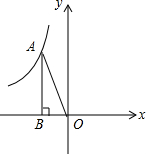 ��ͼ������������y=$\frac{k}{x}$�ڵڶ�����ͼ������һ��A������A��AB��x����B����S��AOB=2����k��ֵΪ��������
��ͼ������������y=$\frac{k}{x}$�ڵڶ�����ͼ������һ��A������A��AB��x����B����S��AOB=2����k��ֵΪ��������| A�� | -4 | B�� | 2 | C�� | -2 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ABC�У�AD�ǡ�ABC�����ߣ���E��AD���е㣬����BE���ӳ�����AC�ڵ�F��
��ͼ����ABC�У�AD�ǡ�ABC�����ߣ���E��AD���е㣬����BE���ӳ�����AC�ڵ�F���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5x+7=7-2x | B�� | 6x-8=8x-4 | C�� | 4x-2=2 | D�� | $\frac{x-3}{-5}$=$\frac{3x+4}{15}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | 5 | B�� | 20 | C�� | 25 | D�� | 18 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com