
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
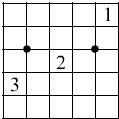 在图5×5和方格中,沿着已有的线画一个简单连续的闭合圈作篱笆,篱笆不能“自身相交”.小方格中的数表示这小方格上属于篱笆的边数(如
在图5×5和方格中,沿着已有的线画一个简单连续的闭合圈作篱笆,篱笆不能“自身相交”.小方格中的数表示这小方格上属于篱笆的边数(如 ),篱笆经过两个黑点,而且对于以“黑点”为中心的长方形,它边上的篱笆也以这个黑点为对称中心.
),篱笆经过两个黑点,而且对于以“黑点”为中心的长方形,它边上的篱笆也以这个黑点为对称中心.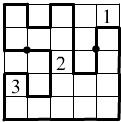

查看答案和解析>>
科目:初中数学 来源:新课标3维同步训练与评价 数学(北师大版·七年级下册) 题型:044
如图所示,直线AB不经过长方形的中心O,与长方形交于C,D两点,作出这个长方形的中心O关于对称轴AB的对称点并作出这个长方形关于对称轴AB的对称图形.

查看答案和解析>>
科目:初中数学 来源: 题型:013
下列说法错误的是
[ ]
A.平行四边形、长方形、正方形都是中心对称图形,对角线的交点是它们的对称中心
B.旋转对称图形不一定是中心对称图形
C.如果两个图形的对应点连成的线段都经过某一点,那么这两个图形一定关于这一点成中心对称
D.在成中心对称的两个图形中,连结对称点的线段都经过对称中心
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com