
分析 (1)设每部B型号的手机x元,则A型号的手机(x+100)元,根据1500元购进A型号手机的数量与用1200元购进B型号手机的数量相同列出方程,求出方程的解即可得到结果;
(2)设B种型号的手机购进a部,则A种型号的手机购进(6-a)部,根据花费的钱数小于等于2900列出不等式,求出不等式的解集的正整数解,即可确定出购机方案;
(3)要获得最大利润,在保证A型手机和B型手机数量均为正整数的条件下A型手机进货越多越好,根据A型手机与B型手机的单价,确定出购机方案即可.
解答 解:(1)设每部B型号的手机x元,则A型号的手机(x+100)元,
根据题意得:$\frac{1500}{x+100}$=$\frac{1200}{x}$,
解得:x=400,
经检验:x=400是原分式方程的解,且x+100=500(元),
答:每部A型手机500元,每部B型手机400元;
(2)设B种型号的手机购进a部,则A种型号的手机购进(6-a)部,
根据题意得:400a+500(6-a)≤2900,
解得:a≥1,
由题意可得a≤5,
∴1≤a≤5,
∵a为解集内的正整数,
∴a=1,2,3,4,5,
∴有5种购机方案:
方案一:A种型号的手机购进5部,则B种型号的手机购进1部;
方案二:A种型号的手机购进4部,则B种型号的手机购进2部;
方案三:A种型号的手机购进3部,则B种型号的手机购进3部;
方案四:A种型号的手机购进2部,则B种型号的手机购进4部;
方案五:A种型号的手机购进1部,则B种型号的手机购进5部;
(3)设购进A种型号的手机m部,购进B种型号的手机n部.
根据题意,得500m+400n=12400,m=$\frac{124-4n}{5}$,
设获得的总利润为w元,则w=100m+90n=100×$\frac{124-4n}{5}$+90n=10n+2480,
∴w随n的增大而增大.
∵m、n均为正整数,
∴当n=26时,能获得最大利润.此时m=$\frac{124-4n}{5}$=$\frac{124-4×26}{5}$=4.
因此,购进A种型号的手机4部,购进B种型号的手机26部时,获利最大.
答:购进A种型号的手机4部,购进B种型号的手机26部时获利最大.
点评 此题考查了分式方程的应用,以及一元一次不等式的运用,抓住题中的关键字眼“用1500元购进A型号手机的数量与用1200元购进B型号手机的数量相同”;“钱可用尽,也可有剩余”;“购进手机,获利最大”是解本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
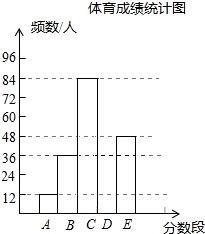 为了了解某市九年级学生的体育成绩(成绩均为整数),随机抽取了部分学生的体育成绩并分段(A:20.5~22.5;B:22.5~24.5;C:24.5~26.5;D:26.5~28.5;E:28.5~30.5)统计,得到统计图、表如下.
为了了解某市九年级学生的体育成绩(成绩均为整数),随机抽取了部分学生的体育成绩并分段(A:20.5~22.5;B:22.5~24.5;C:24.5~26.5;D:26.5~28.5;E:28.5~30.5)统计,得到统计图、表如下.| 分数段 | A | B | C | D | E | 合计 |
| 频数/人 | 12 | 36 | 84 | b | 48 | c |
| 频率 | 0.05 | a | 0.35 | 0.25 | 0.20 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 采购数量(件) | 1 | 2 | … |
| A产品单价(元/件) | 250 | 230 | … |
| B产品单价(元/件) | 130 | 120 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com