练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    4．32015+5除以32012-1，所得的余数是（　　）
    A．313-1B．311-1C．32D．8

    分析 把分子变形：变成有因数为32012-1的形式，所以把5化为32-27=32-33，则：$\frac{{3}^{2015}+5}{{3}^{2012}-1}$=$\frac{{3}^{3}×{3}^{2012}-{3}^{3}+32}{{3}^{2012}-1}$，分子再提公因式，相除得结果．

    解答 解：$\frac{{3}^{2015}+5}{{3}^{2012}-1}$，
    =$\frac{{3}^{3}×{3}^{2012}-{3}^{3}+32}{{3}^{2012}-1}$，
    =$\frac{{3}^{3}（{3}^{2012}-1）+32}{{3}^{2012}-1}$，
    =27…32，
    所以32014+5除以32012-1，所得的余数是32，
    故选C．

    点评 本题因式分解的应用，考查了利用因式分解进行指数幂的运算，通过相等关系的变形：5=32-27，与提公因式相结合，同时要熟练掌握有余除法的计算过程，从而得出结论．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    8．若二次函数的图象过（-3，0）、（1，0）、（0，-3）三点，求这个二次函数的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．计算：$\frac{\sqrt{15}}{\sqrt{6}}$×（-5$\sqrt{2\frac{2}{7}}$）÷2$\sqrt{28}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．下列运算正确的是（　　）
    A．$\sqrt{25}$=±5B．4$\sqrt{3}$-$\sqrt{27}$=1C．$\sqrt{24}$•$\sqrt{\frac{3}{2}}$=6D．$\sqrt{18}$÷$\sqrt{2}$=9

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．如图，有一段斜坡BC长为10米，坡角∠CBD=12°，为方便残疾人的轮椅车通行，现准备把坡角降为5°．
    参考数据  α=5° α=12°
     sinα 0.09 0.21
     cosα 0.10 0.98
     tanα 0.090.21
    （1）求坡高CD；
    （2）求斜坡新起点A与原起点B的距离AB（精确到0.1米）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．设设2001=${2}^{{a}_{1}}+{2}^{{a}_{2}}+{2}^{{a}_{3}}+…+{2}^{{a}_{n}}$，其中a1，a2，a3，…an为彼此两两不等的非负整数，则a1+a2+a3+…+an=44．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．已知函数y=（m2-4）x${\;}^{{m}^{2}-m-4}$+（m-3）x+2是二次函数，求它的解析式，并求出该二次函数的最大值或最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

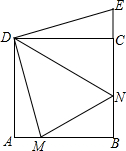    13．如图，在正方形ABCD中，AB=4，∠MDN=45°，点M，N分别在AB，BC边上，延长BC至E，使CE=AM，连接DE．
    （1）求证：DM=DE；
    （2）猜想MN，AM，CN之间有什么数量关系，并进行证明；
    （3）设AM=t，若△MDN为等腰三角形，请直接写出t的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．解方程：
    （1）x2-3x-2=0     
    （2）（x-3）2=4x（x-3）
    （3）$\frac{x}{x-2}$=$\frac{3（x-2）}{x}$+2．

    查看答案和解析>>

    同步练习册答案