
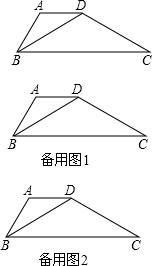
 如图,在梯形纸片ABCD中,AD∥BC,AD=AB=4,BD=CD,∠C=30°,E为BC边上一点,以BE为直角边,E为直角顶点作等腰Rt△BEF,使等腰Rt△BEF和梯形ABCD在BC的同侧.
如图,在梯形纸片ABCD中,AD∥BC,AD=AB=4,BD=CD,∠C=30°,E为BC边上一点,以BE为直角边,E为直角顶点作等腰Rt△BEF,使等腰Rt△BEF和梯形ABCD在BC的同侧.分析 (1)作辅助线构建直角三角形,可得∠ADB=30°,设BE=x,依次把EF、DG、BD、DC表示出来,利用30°角直角三角形所对的直角边是斜边的一半得AH的长,利用勾股定理求DH,从而求出BD的长,列式计算即可;
(2)不存在,如图2,可求得∠EMF′=60°,是一个定值,因此如果△EMF′中任意两边相等时,它都为等边三角形,列式求得t为负数,不符合题意,所以不存在;
(3)分两种情况:①当0≤t<6-2$\sqrt{3}$时,重叠部分的面积为四边形面积,利用差来求;②当6-2$\sqrt{3}$≤t≤12-2$\sqrt{3}$时,如图4,重叠部分的图形为四边形MB′EN,利用两三角形的面积差求.
解答 解:(1)如图1,设BE=x,
∵△BEF为等腰直角三角形,
∴EF=BE=x,
过D作DG⊥BC于G,过A作AH⊥BD于H,则DG=x,DC=BC=2x,
∵DC=BC,
∴∠DBC=∠C=30°,
∵AD∥BC,
∴∠ADB=∠DBC=30°,
在Rt△AHD中,AD=4,则AH=2,DH=2$\sqrt{3}$,
∴BD=2DH=4$\sqrt{3}$,
则2x=4$\sqrt{3}$,x=2$\sqrt{3}$,
∴BE=2$\sqrt{3}$;
(2)不存在,如图2,理由是:
∵∠ADB=30°,
∴∠FMD=60°,
∵F与F′关于BD对称,
∴∠DMF′=∠FMD=60°,
∴∠EMF′=60°,
则△EMF′中任意两边相等时,它都为等边三角形;
设BM=x,则FM=F′M=2$\sqrt{3}$-x,
∴x=2$\sqrt{3}$-x,x=$\sqrt{3}$,
在Rt△BEM中,∠DBC=30°,
∴BE=3,
∴t=3-2$\sqrt{3}$<0,不符合题意;
∴不存在这样的t,使△F′EM是等腰三角形;
(3)①当0≤t<6-2$\sqrt{3}$时,如图3,过M作MN⊥BC于N,
设MN=x,则B′N=MN=x,
tan30°=$\frac{MN}{BN}$=$\frac{x}{x+t}$=$\frac{\sqrt{3}}{3}$,
x=$\frac{(\sqrt{3}+1)t}{2}$,即MN=$\frac{(\sqrt{3}+1)t}{2}$,
tan30°=$\frac{EG}{BE}$=$\frac{EG}{2\sqrt{3}+t}$=$\frac{\sqrt{3}}{3}$,
∴EG=2+$\frac{\sqrt{3}t}{3}$,
∴S=S△BGE-S△BB′M=$\frac{1}{2}$(2$\sqrt{3}$+t)(2+$\frac{\sqrt{3}t}{3}$)-$\frac{1}{2}$t•$\frac{(\sqrt{3}+1)t}{2}$,
S=$\frac{(-3-\sqrt{3}){t}^{2}}{12}$+2t+2$\sqrt{3}$;
②当6-2$\sqrt{3}$≤t≤12-2$\sqrt{3}$时,如图4,重叠部分的图形为四边形MB′EN,
设GN=x,则FG=$\sqrt{3}x$,EC=12-t-2$\sqrt{3}$,
cos30°=$\frac{EN}{EC}$,
∴EN=$\frac{\sqrt{3}}{3}$(12-t-2$\sqrt{3}$)=4$\sqrt{3}$-$\frac{\sqrt{3}t}{3}$-2,
∴EF=FN+EN,
2$\sqrt{3}$=$\sqrt{3}$x+x+4$\sqrt{3}$-$\frac{\sqrt{3}t}{3}$-2,
x=$\frac{3-\sqrt{3}}{6}$t-4,
则S=S△B′EF-S△MNF=$\frac{1}{2}$×2$\sqrt{3}$×$2\sqrt{3}$-$\frac{1}{2}$($\sqrt{3}+1)$x$•\sqrt{3}$x=6-$\frac{1}{2}$(3+$\sqrt{3}$)($\frac{3-\sqrt{3}}{6}$t-4)2.
点评 本题是四边形的综合题,计算量较大;考查了梯形、等腰直角三角形的性质,考查了30°的直角三角形的特殊性质,这一性质应用较多,要熟练掌握;对于重叠部分的面积要根据图形特点分类讨论并利用面积公式代入求解.


科目:初中数学 来源: 题型:选择题
| A. | 7,24,25 | B. | 3,4,$\frac{14}{3}$ | C. | 3,4,5 | D. | 15,8,17 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
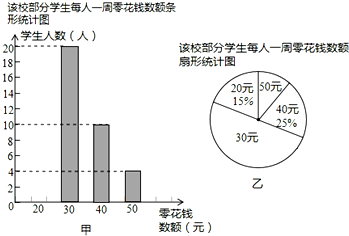
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
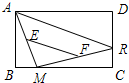 如图,矩形ABCD中,点R沿CD边从点C向点D运动,点M在BC边上运动,E、F分别是AM、MR的中点,则EF的长度随着点M、点R的运动( )
如图,矩形ABCD中,点R沿CD边从点C向点D运动,点M在BC边上运动,E、F分别是AM、MR的中点,则EF的长度随着点M、点R的运动( )| A. | 变短 | B. | 变长 | C. | 不变 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
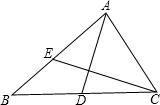 如图,D、E分别是△ABC的边BC和AB上的点,△ABD与△ACD的周长相等,△CAE与△CBE的周长相等,设BC=a,AC=b,AB=c,给出以下几个结论:
如图,D、E分别是△ABC的边BC和AB上的点,△ABD与△ACD的周长相等,△CAE与△CBE的周长相等,设BC=a,AC=b,AB=c,给出以下几个结论:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a2-4(-a+1)=a2-4a-4 | B. | -(mn-1)+(m-n)=-mn-1+m-n | ||
| C. | 5x-(2x-1)-x2=5x-2x+1-x2 | D. | x2-2(2x-y+2)=x2-4x+y-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com