
【题目】如图,OF是∠MON的平分线,点A在射线OM上,P,Q是直线ON上的两动点,点Q在点P的右侧,且PQ=OA,作线段OQ的垂直平分线,分别交直线OF,ON于点B、点C,连接AB,PB.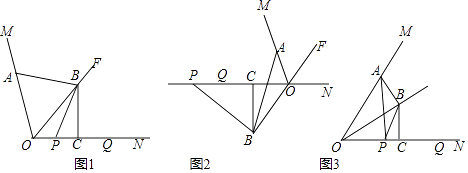
(1)如图1,当P、Q两点都在射线ON上时,请直接写出线段AB与PB的数量关系;
(2)如图2,当P、Q两点都在射线ON的反向延长线上时,线段AB,PB是否还存在(1)中的数量关系?若存在,请写出证明过程;若不存在,请说明理由;
(3)如图3,∠MON=60°,连接AP,设 ![]() =k,当P和Q两点都在射线ON上移动时,k是否存在最小值?若存在,请直接写出k的最小值;若不存在,请说明理由.
=k,当P和Q两点都在射线ON上移动时,k是否存在最小值?若存在,请直接写出k的最小值;若不存在,请说明理由.
【答案】
(1)解:连接:AB=PB.
理由:如图1中,连接BQ.
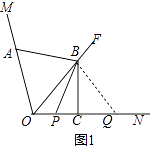
∵BC垂直平分OQ,
∴BO=BQ,
∴∠BOQ=∠BQO,
∵OF平分∠MON,
∴∠AOB=∠BQO,
∵OA=PQ,
∴△AOB≌△PQB,
∴AB=PB.
(2)解:存在,
理由:如图2中,连接BQ.
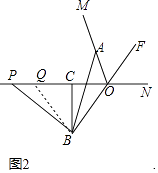
∵BC垂直平分OQ,
∴BO=BQ,
∴∠BOQ=∠BQO,
∵OF平分∠MON,∠BOQ=∠FON,
∴∠AOF=∠FON=∠BQC,
∴∠BQP=∠AOB,
∵OA=PQ,
∴△AOB≌△PQB,
∴AB=PB.
(3)解:连接BQ.
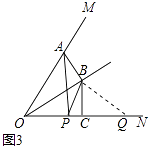
易证△ABO≌△PBQ,
∴∠OAB=∠BPQ,AB=PB,
∵∠OPB+∠BPQ=180°,
∴∠OAB+∠OPB=180°,∠AOP+∠ABP=180°,
∵∠MON=60°,
∴∠ABP=120°,
∵BA=BP,
∴∠BAP=∠BPA=30°,
∵BO=BQ,
∴∠BOQ=∠BQO=30°,
∴△ABP∽△OBQ,
∴ ![]() =
= ![]() ,
,
∵∠AOB=30°,
∴当BA⊥OM时, ![]() 的值最小,最小值为0.5,
的值最小,最小值为0.5,
∴k=0.5.
【解析】(1)利用垂直平分线的性质须连结BQ,构造出全等三角形;(2)类比(1)的方法、辅助线做法,仍是构造全等三角形;(3)连结BQ,转化整个比例,通过相似,转化![]() 为
为![]() ,从而当垂直时比值最小,恰等于sin30°=0.5.
,从而当垂直时比值最小,恰等于sin30°=0.5.
【考点精析】通过灵活运用线段垂直平分线的性质和相似三角形的判定与性质,掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方即可以解答此题.


科目:初中数学 来源: 题型:
【题目】如图,圆柱形容器中,高为1.2m,底面周长为1m,在容器内壁离容器底部0.3m的点B处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿0.3m与蚊子相对的点A处,则壁虎捕捉蚊子的最短距离为 m(容器厚度忽略不计).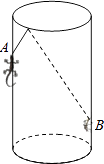
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,延长AB至E,延长CD至F,BE=DF,连接EF,与BC、AD分别相交于P、Q两点.
(1)求证:CP=AQ;
(2)若BP=1,PQ=![]() ,∠AEF=45°,求矩形ABCD的面积.
,∠AEF=45°,求矩形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料: 小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:![]() ,善于思考的小明进行了以下探索:
,善于思考的小明进行了以下探索:
设![]() (其中
(其中![]() 均为整数),则有
均为整数),则有![]() .
.
∴![]() .这样小明就找到了一种把部分
.这样小明就找到了一种把部分![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
当![]() 均为正整数时,若
均为正整数时,若![]() ,用含m、n的式子分别表示
,用含m、n的式子分别表示![]() ,得
,得![]() = ,
= ,![]() = ;
= ;
(2)利用所探索的结论,找一组正整数![]() ,填空: + =( +
,填空: + =( + ![]() )2;
)2;
(3)若![]() ,且
,且![]() 均为正整数,求
均为正整数,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一架梯子AB斜靠在墙面上,且AB的长为25米.
(1)若梯子底端离墙角的距离OB为7米,求这个梯子的顶端A距地面有多高?
(2)在(1)的条件下,如果梯子的顶端A下滑4米到点A,,那么梯子的底端B在水平方向滑动的距离BB,为多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P为反比例函数y= ![]() (k>0)在第一象限内图象上的一点,过点P分别作x轴,y轴的垂线交一次函数y=﹣x﹣4的图象于点A,B.若∠AOB=135°,则k的值是( )
(k>0)在第一象限内图象上的一点,过点P分别作x轴,y轴的垂线交一次函数y=﹣x﹣4的图象于点A,B.若∠AOB=135°,则k的值是( )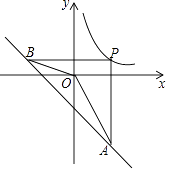
A.2
B.4
C.6
D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一张长方形的桌子可坐6人,按下图将桌子拼起来.

按这样规律做下去:(1)有5张桌子时可坐 人;
(2)有10张桌子时可坐 人;
(3)有n张桌子可以坐 人(用含有n的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把2张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为m,宽为n)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示.阴影部分刚好能分割成两张形状大小不同的小长方形卡片(如图③),则分割后的两个阴影长方形的周长和是( )
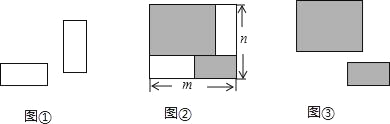
A. 4mB. 2(m+n)C. 4nD. 4(m﹣n)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com