
分析 由点A的坐标可得,OA与y轴的夹角为45°,若点P在y轴上,△AOP构成的等腰三角形,应分OA是腰和是底,以及是等腰直角三角形还是普通等腰三角形来讨论.
解答 解:∵A(2,-2)
∴OA=$\sqrt{{2}^{2}{+2}^{2}}$=2$\sqrt{2}$,OA与y轴的夹角为45°
①当点P在y轴的正半轴上时,OP=OA=2$\sqrt{2}$,则点P的坐标为(0,2$\sqrt{2}$);
②当△AOP为等腰直角三角形时,且OA是斜边时,OP=PA=2,则点P的坐标为(0,-2);
③当△AOP为等腰直角三角形时,且OA是直角边时,OA=PA=2$\sqrt{2}$,OP=4,则点P的坐标为(0,-4);
④当点P在y轴的负半轴上时,且OA=OP=2$\sqrt{2}$,则点P的坐标为(0,-2$\sqrt{2}$).
综上所述,符合条件P点的坐标有:4;(0,2$\sqrt{2}$)或(0,-2)或(0,-$\sqrt{2}$)或(0,-4).
点评 本题考查了等腰三角形的性质,注意应分四种情况讨论是解答此题的关键.


 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:解答题
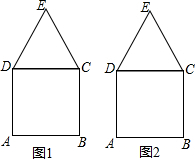 如图,已知正方形ABCD和等边三角形CDE,请按要求完成下列画图,要求:①仅用无刻度的直尺,②保留必要的画图痕迹.
如图,已知正方形ABCD和等边三角形CDE,请按要求完成下列画图,要求:①仅用无刻度的直尺,②保留必要的画图痕迹.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2-x}{1-x}$ | B. | x+1 | C. | x-1 | D. | $\frac{1}{2-x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com