
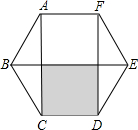
 (2012•台湾)如图,正六边形ABCDEF的边长为1,连接AC、BE、DF,求图中灰色四边形的周长为何?( )
(2012•台湾)如图,正六边形ABCDEF的边长为1,连接AC、BE、DF,求图中灰色四边形的周长为何?( ) 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
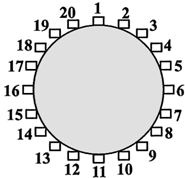 (2012•台湾)如图,一圆桌周围有20个箱子,依顺时针方向编号1~20.小明在1号箱子中丢入一颗红球后,沿着圆桌依顺时针方向行走,每经过一个箱子就依下列规则丢入一颗球:
(2012•台湾)如图,一圆桌周围有20个箱子,依顺时针方向编号1~20.小明在1号箱子中丢入一颗红球后,沿着圆桌依顺时针方向行走,每经过一个箱子就依下列规则丢入一颗球:查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•台湾)如图,坐标平面上直线L的方程式为3x-y=-3.若有一直线L′的方程式为y=a,则a的值在下列哪一个范围时,L′与L的交点会在第二象限?( )
(2012•台湾)如图,坐标平面上直线L的方程式为3x-y=-3.若有一直线L′的方程式为y=a,则a的值在下列哪一个范围时,L′与L的交点会在第二象限?( )查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
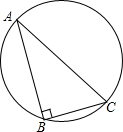 (2012•台湾)如图,直角三角形ABC有一外接圆,其中∠B=90°,AB>BC,今欲在
(2012•台湾)如图,直角三角形ABC有一外接圆,其中∠B=90°,AB>BC,今欲在 |
| BC |
 |
| BP |
 |
| CP |
 |
| BC |
 |
| BC |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com