
【题目】如图,在平面直角坐标系中,已知Rt△AOB的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,且OA、OB的长满足|OA﹣8|+(OB﹣6)2=0,∠ABO的平分线交x轴于点C过点C作AB的垂线,垂足为点D,交y轴于点E.
(1)求线段AB的长;
(2)求直线CE的解析式;
(3)若M是射线BC上的一个动点,在坐标平面内是否存在点P,使以A、B、M、P为顶点的四边形是矩形?若存在,请直接写出点P的坐标;若不存在,请说明理由.

【答案】(1)求线段AB=10;(2)求直线CE的解析式y=-![]() x-4;(3)点P的坐标(-4,8)、(3,2);
x-4;(3)点P的坐标(-4,8)、(3,2);
【解析】试题分析:
(1) 根据绝对值和平方的非负性可以获得线段OA和OB的长. 利用勾股定理可以得到线段AB的长.
(2) 要求直线CE的解析式,需要先求点C和点E的坐标. 利用角平分线的性质可以得到OB=DB,OC=DC. 利用已知的线段长度和各线段之间的关系,在Rt△ADC中通过勾股定理可以获得关于OC的方程,求解这一方程即可获得点C的坐标. 利用对顶角的关系可以证明△ADC与△EOC全等,进而可以利用线段AD的长获得点E的坐标. 利用点C和点E的坐标通过待定系数法即可求得直线CE的解析式.
(3) 根据题意可以在第一和第二象限内各找到一个符合题意的点P. 因此,本小题应该对这两种情况分别进行讨论. 在求解位于第二象限内的点P坐标的时候,可以过点P作y轴的垂线PG. 利用△BOC和△AMC相似的关系获得线段AM的长,利用矩形的性质得到线段PB的长. 利用△PGB与△BOC相似的关系获得线段PG和BG的长,进而写出点P的坐标. 在求解位于第一象限内的点P坐标的时候,可以过点P作y轴的垂线PH. 利用△ABM与△DBC相似的关系获得线段AM的长,利用矩形的性质得到线段PB的长. 利用△PHB与△BOA相似的关系获得线段PH和BH的长,进而写出点P的坐标.
试题解析:
(1) ∵![]() ,
,
∴OA=8,OB=6.
∴在Rt△AOB中, ![]() .
.
(2) 设OC=m,则AC=OA-OC=8-m.
∵点C在∠ABO的平分线上,
∴![]() .
.
∵OC⊥BE,CD⊥AB,
∴∠BOC=∠BDC=90°.
∵在△BOC和△BDC中,
 ,
,
∴△BOC≌△BDC (AAS).
∴OB=DB=6,OC=DC=m.
∴AD=AB-BD=10-6=4.
∵在Rt△ADC中,AC2=AD2+CD2,
∴(8-m)2=42+m2,
∴m=3.
∴OC=m=3.
∴点C的坐标为(-3, 0).
∵在△ADC和△EOC中,
 ,
,
∴△ADC≌△EOC (ASA).
∴AD=EO=4.
∴点E的坐标为(0, -4).
设直线CE的解析式为y=kx+b (k≠0).
将点C和点E的坐标分别代入直线CE的解析式,得
![]() ,
,
解之,得
 ,
,
∴直线CE的解析式为![]() .
.
(3) 点P的坐标为(-4, 8)或(3, 2). 求解过程如下.
根据题意,分别对下面两种情况进行讨论.

①如图①,四边形AMBP为矩形.
过点P作PG⊥OB,垂足为G.
∵OC=3,OB=6,
∴在Rt△BOC中, ![]() .
.
∵∠BOC=∠AMC=90°,∠BCO=∠ACM,
∴△BOC∽△AMC,
∴![]() .
.
∵AC=OA-OC=8-3=5,OB=6, ![]() ,
,
∴![]() .
.
∴在矩形AMBP中, ![]() .
.
∵∠PBM=90°,
∴∠PBG+∠OBC=180°-∠PBM=180°-90°=90°.
∵在Rt△BOC中,∠BCO+∠OBC=90°,
∴∠PBG=∠BCO.
∵∠PGB=∠BOC=90°,∠PBG=∠BCO,
∴△PGB∽△BOC,
∴![]() .
.
∴![]() ,
, ![]() .
.
∴OG=OB+BG=6+2=8.
∴点P的坐标为(-4, 8).
②如图②,四边形AMBP为矩形.
如图②,过点P作PH⊥OB,垂足为H.
∵CD⊥AB,AM⊥AB,
∴CD∥AM,
∴△ABM∽△DBC,
∴![]() .
.
∵CD=OC=3,BD=OB=6,AB=10,
∴![]() .
.
∴在矩形AMBP中,BP=MA=5.
∵∠ABO+∠PBH=∠ABP=90°,
又∵在Rt△AOB中,∠ABO+∠BAO=90°,
∴∠PBH=∠BAO.
∵∠PHB=∠BOA=90°,∠PBH=∠BAO,
∴△PHB∽△BOA,
∴![]() .
.
∴![]() ,
, ![]() .
.
∴OH=OB-BH=6-4=2.
∴点P的坐标为(3, 2).
综上所述,点P的坐标为(-4, 8)或(3, 2).


科目:初中数学 来源: 题型:
【题目】因式分解4a3-a的结果是( )
A. a(4a2-1) B. a(2a-1)2 C. a(2a+1)(2a-1) D. 4a(a+1)(a-1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A6B6A7的边长为( ) 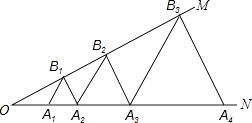
A.6
B.12
C.32
D.64
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高校共有5个大餐厅和2个小餐厅.经过测试:同时开放1个大餐厅、2个小餐厅,可供1680名学生就餐;同时开放2个大餐厅、1个小餐厅,可供2280名学生就餐.
(1)求1个大餐厅、1个小餐厅分别可供多少名学生就餐;
(2)若7个餐厅同时开放,能否供全校的5300名学生就餐?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
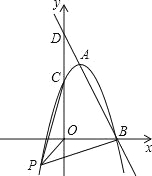
【题目】如图,已知直线y=kx+6与抛物线y=![]() +bx+c相交于A,B两点,且点A(1,4)为抛物线的顶点,点B在x轴上.
+bx+c相交于A,B两点,且点A(1,4)为抛物线的顶点,点B在x轴上.
(1)求抛物线的解析式;
(2)在(1)中抛物线的第三象限图象上是否存在一点P,使△POB与△POC全等?若存在,求出点P的坐标;若不存在,请说明理由;
(3)若点Q是y轴上一点,且△ABQ为直角三角形,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ABC=90°,以AB为直径作半圆⊙O交AC与点D,点E为BC的中点,连接DE.
(1)求证:DE是半圆⊙O的切线.
(2)若∠BAC=30°,DE=2,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某兴趣小组决定去市场购买A,B,C三种仪器,其单价分别为3元,5元,7元,购买这批仪器需花62元;经过讨价还价,最后以每种单价各下降1元成交,结果只花50元就买下了这批仪器.那么A种仪器最多可买( )
A.8件
B.7件
C.6件
D.5件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com