
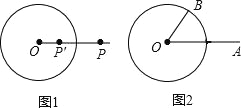
【题目】如图1,⊙O的半径为r(r>0),若点P′在射线OP上,满足OP′OP=r2,则称点P′是点P关于⊙O的“反演点”.
如图2,⊙O的半径为4,点B在⊙O上,∠BOA=60°,OA=8,若点A′,B′分别是点A,B关于⊙O的反演点,求A′B′的长.
科目:初中数学 来源: 题型:
【题目】世界文化遗产长城总长约6700000m,6700000用科学记数法可表示为( )
A.6.7×105B.67×105C.6.7×106D.67×106
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是由若干个小圆圈堆成的一个形如等边三角形的图案,最上面一层有一个圆圈,以下各层均比上一层多一个圆圈,一共堆了n层.将图1倒置后与原图1拼成图2的形状,这样我们可以算出图1中所有圆圈的个数为1+2+3+…+n= ![]() .
.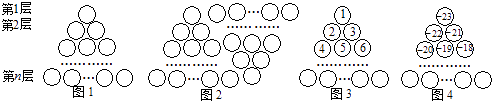
如果图中的圆圈共有11层,请问:自上往下,在每个圆圈中按图3的方式填上一串连续的正整数1,2,3,4,…,则最底层中间这个圆圈中的数是;自上往下,在每个圆圈中按图4的方式填上一串连续的整数
﹣23,﹣22,﹣21,﹣20,…,则所有圆圈中各数之和为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=ax+b(a>0)与x轴的交点坐标为(m,0),则一元一次不等式ax+b≤0的解集应为( )
A. x≤m B. x≤-m C. x≥m D. x≥-m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,A,E,F,C在一条直线上,AE=CF,过点E,F分别作DE⊥AC,BF⊥AC,且AB=CD.
(1)求证:BD平分EF.
(2)若将△DEC的边EC沿AC方向移动变为图②,其余的条件不变,上述结论是否仍成立?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读以下内容,并回答问题:
若一个三角形的两边平方和等于第三边平方的两倍,我们称这样的三角形为奇异三角形.
(1)命题“等边三角形一定是奇异三角形”是 命题(填“真”或“假”);
(2)在△ABC中,已知∠C=90°,△ABC的内角∠A、∠B、∠C所对边的长分别为a、b、c,且b>a,若Rt△ABC是奇异三角形,求a:b:c;
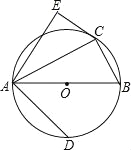
(3)如图,已知AB是⊙O的直径,C是⊙O上一点(点C与点A、B不重合),D是半圆![]() 的中点,C、D在直径AB的两侧,若存在点E,使AE=AD,CB=CE.求证:△ACE是奇异三角形.
的中点,C、D在直径AB的两侧,若存在点E,使AE=AD,CB=CE.求证:△ACE是奇异三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
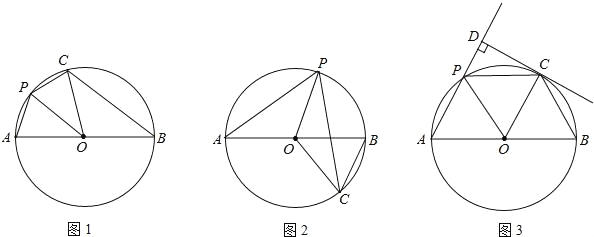
【题目】已知,AB是⊙O的直径,点P在弧AB上(不含点A、B),把△AOP沿OP对折,点A的对应点C恰好落在⊙O上.
(1)当P、C都在AB上方时(如图1),判断PO与BC的位置关系(只回答结果);
(2)当P在AB上方而C在AB下方时(如图2),(1)中结论还成立吗?证明你的结论;
(3)当P、C都在AB上方时(如图3),过C点作CD⊥直线AP于D,且CD是⊙O的切线,证明:AB=4PD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小明遇到这样一个问题:
如图1,△ABC中,∠A=90°,∠B=30°,点D,E分别在AB,BC上,且∠CDE=90°.当BE=2AD时,图1中是否存在与CD相等的线段?若存在,请找出并加以证明,若不存在,说明理由.
小明通过探究发现,过点E作AB的垂线EF,垂足为F,能得到一对全等三角形(如图2),从而将解决问题.
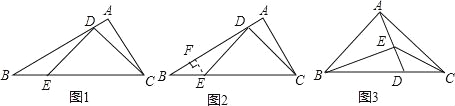
请回答:
(1)小明发现的与CD相等的线段是 .
(2)证明小明发现的结论;
参考小明思考问题的方法,解决下面的问题:
(3)如图3,△ABC中,AB=AC,∠BAC=90°,点D在BC上,BD=2DC,点E在AD上,且∠BEC=135°,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com