
【题目】如图,已知AB是⊙O的直径,C是⊙O上的点,点D在AB的延长线上,∠BCD=∠BAC.
(1)求证:CD是⊙O的切线.
(2)若∠D=30°,BD=2,求⊙O的半径
(3)在(2)的条件下,求图中阴影部分的面积.
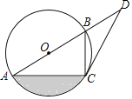
【答案】(1)见解析;(2)2;(3)![]()
【解析】
(1)连接OC,则得∠BAC=∠OCA,结合条件∠BCD=∠BAC证出∠OCD=90°,得OC⊥CD则可证切线;
(2)在Rt△OCD中,利用30°角所对的直角边等于斜边的一半可得OD与半径的关系,列方程求解;
(3)根据弓形面积等于扇形面积减去三角形的面积,分别用公式计算扇形和三角形的面积即可求解.
解:如图,连接![]()
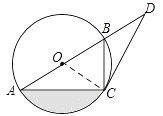
(1)∵OA=OC,
∴∠BAC=∠OCA,
∵∠BCD=∠BAC,
∴![]() ,
,
∵![]() 是直径,
是直径,
∴∠ACB=90°=∠OCA+∠OCB,
∴![]() ,即
,即![]() .
.
∵![]() 是半径,
是半径,
∴CD是⊙O的切线.
(2)设⊙O的半径为r,则![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
由OB+BD=OD得![]() ,
,
解得![]() ,
,
∴⊙O的半径为2.
(3)在![]() 中,∵∠BOC=60°,
中,∵∠BOC=60°,
∴![]() 是正三角形,
是正三角形,
∵OB=OC=2
∴由勾股定理得![]() .
.
∵O为![]() 中点,
中点,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
所以![]() ,
,
所以![]() .
.
故图中阴影部分的面积为![]() .
.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋中有标号为1,2,3,4的四个小球,除数字不同外,小球没有任何区别,摸球前先搅拌均匀,每次摸一个球
(1)摸出一个球,摸到标号为偶数的概率为 .
(2)从袋中不放回地摸两次,用列表或树状图求出两球标号数字为一奇一偶的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=5,CD⊥AB于点D,CD=3.点P从点A出发沿线段AC以每秒1个单位的速度向终点C运动.过点P作PQ∥AB交BC于点Q,过点P作AC的垂线,过点Q作AC的平行线,两线交于点E.设点P的运动时间为t秒.
(1)求线段PQ的长.(用含t的代数式表示)
(2)当点E落在边AB上时,求t的值.
(3)当△PQE与△ACD重叠部分图形是四边形时,直接写出t的取值范围.
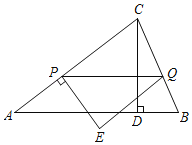
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(知识回顾)
我们把连结三角形两边中点的线段叫做三角形的中位线,并且有:三角形的中位线平行于第三边,并且等于第三边的一半.
(定理证明)
将下列的定理证明补充完整:
已知:如图①,在△ABC中,点D、E分别是边AB、AC中点,连结DE.
求证:
证明:
(定理应用)
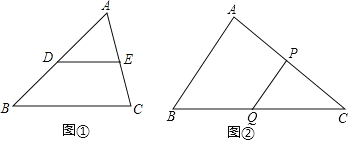
如图②,在△ABC中,AB=10,∠ABC=60°,点P、Q分别是边AC、BC的中点,连结PQ.
(1)线段PQ的长为 .
(2)以点C为一个端点作线段CD(CD与AB不平行),连结AD,取AD的中点M,连结PM、QM.
①在图②中补全图形.
②当∠PQM=∠PMQ时,求CD的长.
③在②的条件下,当△PQM面积最大时,直接写出∠BCD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是一块绿化带,将阴影部分修建为花圃,已知AB=15,AC=9,BC=12,阴影部分是△ABC的内切圆,一只自由飞翔的小鸟将随机落在这块绿化带上,则小鸟落在花圃上的概率为______.
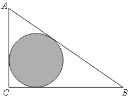
查看答案和解析>>
科目:初中数学 来源: 题型:
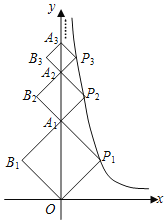
【题目】如图,四边形OP1A1B1,A1P2A2B2,A2P3A3B3,An﹣1PnAnBn都是正方形,其中点A1、A2、A3…An在y轴上,点P1(x1,y1),P2(x2,y2),…,Pn(xn,yn)在反比例函数y=![]() (x>0)的图象上,已知B1(﹣1,1),则点Pn的坐标为( )
(x>0)的图象上,已知B1(﹣1,1),则点Pn的坐标为( )
A.![]() B.
B.![]()
C.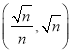 D.
D.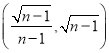
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E为AD边上的一点,过C点作CF⊥CE交AB的延长线于点F.
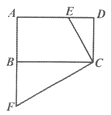
(1)求证:△CDE∽△CBF;
(2)若B为AF的中点,CB=3,DE=1,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经销一种双肩包,已知这种双肩包的成本价每个20元,市场调查发现,这种双肩包每天的销售量![]() (单位:个)与销售单价
(单位:个)与销售单价![]() (单位:元)有如下关系:
(单位:元)有如下关系:![]() (
(![]() )设这种双肩包每天的销售利润为
)设这种双肩包每天的销售利润为![]() 元.
元.
(1)这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(2)如果物价部门规定这种双肩包的销售单价不高于48元,该商店销售这种双肩包每天要获得300元的销售利润,销售单价应定为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com