
 如图①,已知△ABC是等腰三角形,∠BAC=90°,点D是BC的中点,作正方形DEFG,使点A、C分别在DG和DE上,连接AE、BG.
如图①,已知△ABC是等腰三角形,∠BAC=90°,点D是BC的中点,作正方形DEFG,使点A、C分别在DG和DE上,连接AE、BG.分析 (1)由等腰直角三角形的性质及正方形的性质就可以得出△ADE≌△BDG就可以得出结论;
(2)如图2,连接AD,由等腰直角三角形的性质及正方形的性质就可以得出△ADE≌△BDG就可以得出结论.
解答 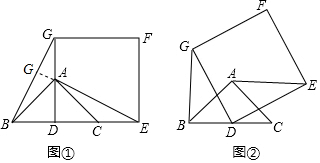 解:(1)BG=AE.AE⊥BG,
解:(1)BG=AE.AE⊥BG,
理由:∵△ABC是等腰直角三角形,∠BAC=90°,点D是BC的中点,
∴AD⊥BC,BD=CD,
∴∠ADB=∠ADC=90°.
∵四边形DEFG是正方形,
∴DE=DG.
在△BDG和△ADE中,
$\left\{\begin{array}{l}{BD=AD}\\{∠BDE=∠ADE}\\{GD=ED}\end{array}\right.$,
∴△ADE≌△BDG(SAS),
∴BG=AE;
∴∠DEA=∠DGB,
∵∠DEA+∠DNE=90°,∠DNE=∠MNG,
∴∠MNG+DGB=90°,
∴AE⊥BG;
(2)成立,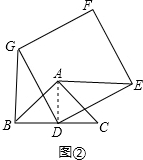
理由:如图②,连接AD,
∵在Rt△BAC中,D为斜边BC中点,
∴AD=BD,AD⊥BC,
∴∠ADG+∠GDB=90°.
∵四边形EFGD为正方形,
∴DE=DG,且∠GDE=90°,
∴∠ADG+∠ADE=90°,
∴∠BDG=∠ADE.
在△BDG和△ADE中,
$\left\{\begin{array}{l}{BD=AD}\\{∠BDG=∠ADE}\\{GD=ED}\end{array}\right.$,
∴△BDG≌△ADE(SAS),
∴BG=AE,
∠AED=∠BGD,
∴∠BGD+DMG=90°,∠DMG=∠EMN
∴∠EMN+∠AED=90°,
∴BG⊥AE.
点评 本题考查了旋转的性质的运用,等腰直角三角形的性质的运用,勾股定理的运用,全等三角形的判定及性质的运用,正方形的性质的运用,解答时证明三角形全等是关键.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | 1 | C. | -1 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α,将△BOC绕点C顺时针方向旋转60°,到△ADC,连接OD.
如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α,将△BOC绕点C顺时针方向旋转60°,到△ADC,连接OD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com