
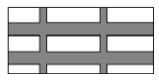
【题目】如图,要设计一幅宽20厘米,长30厘米的图案,其中有两横两竖的彩条,横、竖彩条的宽度比为2∶1,如果要使彩条所占面积是图案面积的一半,那么竖彩条宽度是多少?若设竖彩条宽度是x厘米,则根据题意可列方程_____________.
科目:初中数学 来源: 题型:
【题目】某种型号的温控水箱的工作过程是:接通电源后,在初始温度20℃下加热水箱中的水;当水温达到设定温度80℃时,加热停止;此后水箱中的水温开始逐渐下降,当下降到20℃时,再次自动加热水箱中的水至80℃时,加热停止;当水箱中的水温下降到20℃时,再次自动加热,…,按照以上方式不断循环.
小明根据学习函数的经验,对该型号温控水箱中的水温随时间变化的规律进行了探究.发现水温y是时间x的函数,其中y(单位:℃)表示水箱中水的温度.x(单位:min)表示接通电源后的时间.
下面是小明的探究过程,请补充完整:
(1)下表记录了32min内14个时间点的温控水箱中水的温度y随时间x的变化情况
接通电源后的时间x(单位:min) | 0 | 1 | 2 | 3 | 4 | 5 | 8 | 10 | 16 | 18 | 20 | 21 | 24 | 32 | … |
水箱中水的温度y(单位:℃) | 20 | 35 | 50 | 65 | 80 | 64 | 40 | 32 | 20 | m | 80 | 64 | 40 | 20 | … |
m的值为 ;
(2)①当0≤x≤4时,写出一个符合表中数据的函数解析式 ;
当4<x≤16时,写出一个符合表中数据的函数解析式 ;
②如图,在平面直角坐标系xOy中,描出了上表中部分数据对应的点,根据描出的点,画出当0≤x≤32时,温度y随时间x变化的函数图象:
(3)如果水温y随时间x的变化规律不变,预测水温第8次达到40℃时,距离接通电源 min.

查看答案和解析>>
科目:初中数学 来源: 题型:
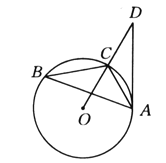
【题目】如图所示,已知△ABC内接于⊙O,点D在OC的延长线上,sin B=![]() ,∠D=30°.
,∠D=30°.
(1)求证AD是⊙O的切线;
(2)若AC=6,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
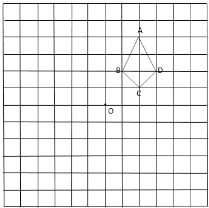
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,已知格点四边形![]() (顶点是网格线的交点)和格点
(顶点是网格线的交点)和格点![]() .
.
(1)将四边形![]() 先向左平移4个单位长度,再向下平移6个单位长度,得到四边形
先向左平移4个单位长度,再向下平移6个单位长度,得到四边形![]() ,画出平移后的四边形
,画出平移后的四边形![]() (点
(点![]() ,
,![]() ,
,![]() ,
,![]() 的对应点分别为点
的对应点分别为点![]() ,
,![]() ,
,![]() ,
,![]() );
);
(2)将四边形![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,得到四边形
,得到四边形![]() ,画出旋转后的四边形
,画出旋转后的四边形![]() (点
(点![]() ,
,![]() ,
,![]() ,
,![]() 的对应点分别为点
的对应点分别为点![]() ,
,![]() ,
,![]() ,
,![]() );
);
(3)填空:点![]() 到
到![]() 的距离为________.
的距离为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市A,B两个蔬菜基地得知四川C,D两个灾民安置点分别急需蔬菜240t和260t的消息后,决定调运蔬菜支援灾区,已知A蔬菜基地有蔬菜200t,B蔬菜基地有蔬菜300t,现将这些蔬菜全部调运C,D两个灾区安置点.从A地运往C,D两处的费用分别为每吨20元和25元,从B地运往C,D两处的费用分别为每吨15元和18元.设从B地运往C处的蔬菜为x吨.
(1)请填写下表,并求两个蔬菜基地调运蔬菜的运费相等时x的值;
C | D | 总计/t | |
A | 200 | ||
B | x | 300 | |
总计/t | 240 | 260 | 500 |
(2)设A,B两个蔬菜基地的总运费为w元,求出w与x之间的函数关系式,并求
总运费最小的调运方案;
(3)经过抢修,从B地到C处的路况得到进一步改善,缩短了运输时间,运费每吨减少m元(m>0),其余线路的运费不变,试讨论总运费最小的调动方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
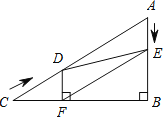
【题目】如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是ts.过点D作DF⊥BC于点F,连接DE、EF.
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,请说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知甲、乙两个长方形纸片,其边长如图中所示![]() ,面积分别为
,面积分别为![]() 和
和![]() .
.

(1)①用含![]() 的代数式表示
的代数式表示![]() _________,
_________,![]() _________;
_________;
②用“![]() ”、“
”、“![]() ”或“
”或“![]() ”号填空:
”号填空:![]() ________
________![]() ;
;
(2)若一个正方形纸片的周长与乙的周长相等,其面积设为![]() .
.
①该正方形的边长是_________(用含![]() 的代数式表示);
的代数式表示);
②小方同学发现,“![]() 与
与![]() 的差是定值”请判断小方同学的发现是否正确,并通过计算说明你的理由.
的差是定值”请判断小方同学的发现是否正确,并通过计算说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形 ABCD 中,AD∥BC,AB=BC,对角线 AC、BD 交于点 O,BD 平分∠ABC,过点 D 作 DE⊥BC 交 BC 的延长线于点 E.连接 OE.
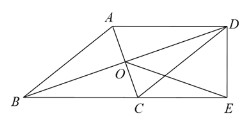
(1)求证:四边形 ABCD 是菱形;
(2)若 tan∠DBC=![]() ,AB=
,AB=![]() ,求线段 OE 的长.
,求线段 OE 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,∠D=30°,AB<AD.
(1)在AD边上求作一点P,使点P到边AB,BC的距离相等;(要求:尺规作图,不写作法,保留作图痕迹)
(2)在(1)的条件下,连接BP,若AB=2,求△ABP的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com