练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    2．把一根长80cm的铁丝分成两个部分，分别围成两个正方形．
    （1）能否使所围的两个正方形的面积和为250cm2，并说明理由；
    （2）能否使所围的两个正方形的面积和为180cm2，并说明理由；
    （3）怎么分，使围成两个正方形的面积和最小？

    分析 （1）设其中一个正方形的边长为x cm，则另一个正方形的边长为（20-x）cm，就可以表示出这两个正方形的面积，根据两个正方形的面积之和等于250cm2建立方程求出其解即可；
    （2）根据题意建立方程x2+（20-x）2=180，再判定该一元二次方程是否有解即可；
    （3）设所围面积和为y cm2，则有y=x2+（20-x）2，再求二次函数最值即可．

    解答 解：（1）设其中一个正方形的边长为x cm，则另一个正方形的边长为（20-x）cm，
    由题意得：x2+（20-x）2=250，
    解得x1=5，x2=15，
    当x=5时，4x=20，4（20-x）=60，
    当x=15时，4x=60，4（20-x）=20，
    答：能，长度分别为20cm与60cm；

    （2）x2+（20-x）2=180，
    整理：x2-20x+110=0，
    ∵b2-4ac=400-440=-40＜0，
    ∴此方程无解，即不能围成两个正方形的面积和为180cm2；

    （3）设所围面积和为y cm2，
    y=x2+（20-x）2，
    =2 x2-40x+400
    =2（ x-10）2+200，
    当x=10时，y最小为200.4x=40，4（20-x）=40，
    答：分成40cm与40cm，使围成两个正方形的面积和最小为200 cm．

    点评 本题考查了列一元二次方程解实际问题的运用，一元二次方程的解法的运用，求二次函数最值的方法，解答本题时找到等量关系建立方程和运用根的判别式是关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    7．已知圆锥底面半径为2，母线长为5，则此圆锥侧面展开图的面积是（　　）
    A．5πB．10πC．7πD．20π

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

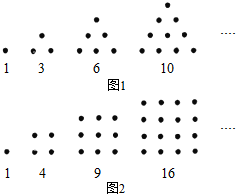    13．古希腊毕达哥拉斯学派的数学家常用小石子在沙滩上摆成各种形状来研究各种多边形数，比如：他们研究过图1中的1，3，6，10，…，由于这些数能够表示成三角形，将其称为三角形数；类似的，称图2中的1，4，9，16，…，这样的数位正方形数（四边形数）．
    （1）请你写出既是三角形数又是正方形数且大于1的最小正整数为36；
    （2）试证明：当k为正整数时，k（k+1）（k+2）（k+3）+1必须为正方形数；
    （3）记第n个k变形数位N（n，k）（k≥3）．例如N（1，3）=1，N（2，3）=3，N（2，4）=4．
    ①试直接写出N（n，3）N（n，4）的表达式；
    ②通过进一步的研究发现N（n，5）=$\frac{3}{2}$n2-$\frac{1}{2}$n，N（n，6）=2n2-n，…，请你推测N（n，k）（k≥3）的表达式，并由此计算N（10，24）的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．今年泉州元宵期间，某数学兴趣小组为了了解游客最喜欢的花灯类型，随机抽取部分游客进行调查，并将调查的结果绘制成下面两幅不完整的统计图：

    （1）本次共抽取的游客人数为1000，“传统”型所对应的圆心角为144°；
    （2）将条形统计图补充完整；
    （3）据了解，今年观赏花灯的游客约100万人，请你估计“最喜欢现代型”花灯的人数是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．某公司销售的一种时令商品每件成本为20元，经过市场调查分析，5月份的日销售件数为：-2t+96（其中t为天数），并且前15天，每天的价格y1（元/件）与时间t（天）的函数关系式为y1=$\frac{1}{4}$t+25（1≤t≤15，且t为整数），第16天到月底每天的价格y2（元/件）与时间t（天）的函数关系式为y2=$\frac{1}{2}$t+40（16≤t≤31，且t为整数），根据以上信息，解答下列问题：
    （1）5月份第10天的销售件数为76件，销售利润为190元；
    （2）请通过计算预测5月份中哪一天的日销售利润w最大，最大日销售利润是多少？
    （3）在实际销售的前15天中，该公司决定每销售一件商品就捐赠m元利润（m＜4）给希望工程．公司通过销售记录发现，前15天中，每天扣除捐赠后的日销售利润w随t的增大而增大，求m的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．某校260名学生读书活动，要求每人每年读课外书4～7本，活动结束后随机调查了部分学生每人的读书量，并分为四种类型．A：4 本；B：5 本；C：6 本；D：7 本．将各类的人数绘制成如下的扇形图（如图 1）和条形图（如图 2），经确认扇形图是正确的，而条形图中尚有一处错误，回答下列问题：
    （I）找出条形图中存在的错误，并画出正确条形图；
    （II）样本数据的众数是5本，中位数是5本；
    （III）计算样本平均数，并根据样本数据，估计这260名学生共读课外书多少本？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．为丰富我校学生的课余生活，增强学生的综合能力，学校计划在下学年新开设A：国际象棋社；B：皮影社；C：话剧社；D：手语社这四个社团；为了解学生喜欢哪一个社团，随机抽取了部分学生进行调查，并将调查结果绘制成如下的条形统计图和扇形统计图，请结合图中信息解答下列问题：

    求样本中喜欢C社团的人数在扇形统计图中的圆心角的度数，并把条形统计图补充完整．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．如图，已知二次函数y=$a{x}^{2}+\frac{3}{2}x+c$的图象与y轴交于点A（0，4），与x轴交于点B，C，点C的坐标为（8，0），连接AB、AC．
    （1）请直接写出二次函数y=$a{x}^{2}+\frac{3}{2}x+c$的表达式；
    （2）判断△ABC的形状，并说明理由；
    （3）若点N在x轴上运动，当以点A、N、C为顶点的三角形是等腰三角形时，请直接写出此时点N的坐标；
    （4）若点N在线段BC上运动（不与点B、C重合），过点N作NM∥AC，交AB于点M，当△AMN面积最大时，求此时点N的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．2015年9月1日，沈丹高速铁路开通运营，让“来一场说走就走的旅行”成为现实．凤城市新建了凤城东站，新建的火车站除有人工普通售票窗口外，新增了自动打印车票的无人售票窗口，某日，从早6点开始到上午9点，每个普通售票窗口售出的车票数y1（张）与售票时间x（小时）的正比例函数关系满足图①中的图象，每个无人售票窗口售出的车票数y2（张）与售票时间x（小时）的函数关系满足图②中的图象．

    （1）图②中图象的前半段（含端点）是以原点为顶点的抛物线的一部分，根据图中所给数据确定抛物线的表达式为y=60x2，其中自变量x的取值范围是0≤x≤$\frac{3}{2}$；
    （2）若当天共开放2个无人售票窗口，截至上午7点，两种窗口共售出的车票数不少于350张，则至少需要开放多少个普通售票窗口？
    （3）上午8点时，每个普通售票窗口与每个无人售票窗口售出的车票数恰好相同．试确定图②中图象的后半段一次函数的表达式．

    查看答案和解析>>

    同步练习册答案