
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=20,BC=15,点D为AC边上的动点,点D从点C出发,沿边CA往A运动,当运动点A时停止,若设点D运动的时间为t秒,点D运动的速度为每秒2个单位长度.
(1)当t=2时,CD= ,AD= ;(请直接写出答案)
(2)当t= 时,△CBD是直角三角形;(请直接写出答案)
(3)求当t为何值时,△CBD是等腰三角形?并说明理由.
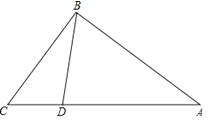
【答案】(1)4,21;(2)4.5或12.5秒;(3)t=6.25或7.5或9秒时,△CBD是等腰三角形.
【解析】试题分析:(1)根据CD=速度×时间列式计算即可得解,利用勾股定理列式求出AC,再根据AD=AC-CD代入数据进行计算即可得解;(2)分①∠CDB=90°时,利用△ABC的面积列式计算即可求出BD,然后利用勾股定理列式求解得到CD,再根据时间=路程÷速度计算;②∠CBD=90°时,点D和点A重合,然后根据时间=路程÷速度计算即可得解;(3)分①CD=BD时,过点D作DE⊥BC于E,根据等腰三角形三线合一的性质可得CE=BE,从而得到CD=AD;②CD=BC时,CD=6;③BD=BC时,过点B作BF⊥AC于F,根据等腰三角形三线合一的性质可得CD=2CF,再由(2)的结论解答.
试题解析:(1)t=2时,CD=2×2=4,
∵∠ABC=90°,AB=20,BC=15,
∴AC=![]() =25,
=25,
AD=ACCD=254=21;
(2)①∠CDB=90°时,S△ABC=![]() ACBD=
ACBD=![]() ABBC,
ABBC,
即![]() ×25BD=
×25BD=![]() ×20×15,
×20×15,
解得BD=12,
所以CD=![]() =9,
=9,
t=9÷2=4.5(秒);
②∠CBD=90°时,点D和点A重合,
t=25÷2=12.5(秒),
综上所述,t=4.5或12.5秒;
故答案为:(1)4,21;(2)4.5或12.5秒;
(3)①CD=BD时,如图1,

过点D作DE⊥BC于E,
则CE=BE,
CD=AD=![]() AC=
AC=![]() ×25=12.5,(或利用余角的性质说明CD=BD=AD)
×25=12.5,(或利用余角的性质说明CD=BD=AD)
t=12.5÷2=6.25;
②CD=BC时,CD=15,t=15÷2=7.5;
③BD=BC时,如图2,

过点B作BF⊥AC于F,
则CF=9,
CD=2CF=9×2=18,
t=18÷2=9,
综上所述,t=6.25或7.5或9秒时,△CBD是等腰三角形.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°
(1)先作∠ACB的平分线交AB边于点P,再以点P为圆心,PA长为半径作⊙P;(要求:尺规作图,保留作图痕迹,不写作法)
(2)请你判断(1)中BC与⊙P的位置关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
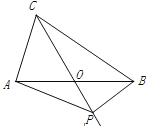
【题目】如图,在△ABC中,AB=BC=4,AO=BO,P是射线CO上的一个动点,∠AOC=60°,则当△PAB为直角三角形时,AP的长为 __________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从一个果园里随机挑选10棵杏树,称得这些杏树的产量分别为(单位:kg):10,15,8,9,12,14,9,10,12,10,若该果园里杏树有100棵,则大约可产杏( )
A. 1 090 kg B. 1 100 kg C. 1 280 kg D. 1 300 kg
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将△ABC的三个顶点的横坐标乘以-1,纵坐标不变,则所得图形( )
A.与原图形关于x轴对称B.与原图形关于y轴对称
C.与原图形关于原点对称D.向y轴的负方向平移了一个单位
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】取一个正整数,若它是奇数,则乘以3加上1,若它是偶数,则除以2,按此规则经过若干步的计算最终可得到1.这个结论在数学上还没有得到证明.但举例验证都是正确的.例如:取自然数5,最少经过下面5步运算可得1,即: ![]() ,如果自然数
,如果自然数![]() 最少经过7步运算可得到1,则所有符合条件的
最少经过7步运算可得到1,则所有符合条件的![]() 的值为______.
的值为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com