
分析 (1)设小王需购买A、B两种品牌文具套装分别为x套、y套,则$\left\{\begin{array}{l}{x+y=1000}\\{20x+25y=22000}\end{array}\right.$,据此求出小王购买A、B两种品牌文具套装分别为多少套即可.
(2)根据题意,可得y=500+0.8×[20x+25(1000-x)],据此求出y与x之间的函数关系式即可.
(3)首先求出小王购买A、B两种品牌文具套装分别为多少套,然后设A品牌文具套装的售价为z元,则B品牌文具套装的售价为z+5元,所以125z+875(z+5)≥20000+8×1000,据此求出A品牌的文具套装每套定价不低于多少元时才不亏本即可.
解答 解:(1)设小王够买A品牌文具x套,够买B品牌文具y套,
根据题意,得:$\left\{\begin{array}{l}{x+y=1000}\\{20x+25y=22000}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=600}\\{y=400}\end{array}\right.$,
答:小王够买A品牌文具600套,够买B品牌文具400套.
(2)y=500+0.8[20x+25(1000-x)]
=500+0.8(25000-5x)
=500+20000-4x
=-4x+20500,
∴y与x之间的函数关系式是:y=-4x+20500.
(3)根据题意,得:-4x+20500=20000,解得:x=125,
∴小王够买A品牌文具套装为125套、够买B品牌文具套装为875套,
设A品牌文具套装的售价为z元,则B品牌文具套装的售价为(z+5)元,
由题意得:125z+875(z+5)≥20000+8×1000,
解得:z≥23.625,
答:A品牌的文具套装每套定价不低于24元时才不亏本.
点评 此题主要考查了一次函数的应用,要熟练掌握,解答此类问题的关键是:(1)简单的一次函数问题:①建立函数模型的方法;②分段函数思想的应用.(2)理清题意是采用分段函数解决问题的关键.


科目:初中数学 来源: 题型:解答题
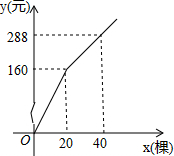 为更新果树品种,某果园计划新购进A、B两个品种的果树苗栽植培育,若计划购进这两种果树苗共45棵,其中A种苗的单价为7元/棵,购买B种苗所需费用y(元)与购买数量x(棵)之间存在如图所示的函数关系.
为更新果树品种,某果园计划新购进A、B两个品种的果树苗栽植培育,若计划购进这两种果树苗共45棵,其中A种苗的单价为7元/棵,购买B种苗所需费用y(元)与购买数量x(棵)之间存在如图所示的函数关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 王师傅开车通过福厦高速公路某隧道(全长约为7千米)时,所走路程为y(千米)与时间x(分钟)之间的函数关系的图象如图所示(A,B,C三点共线).王师傅说:“我开车通过隧道时,有一段连续2分钟恰好走了1.9千米”.你认为王师傅说有可能对吗?请说明理由.
王师傅开车通过福厦高速公路某隧道(全长约为7千米)时,所走路程为y(千米)与时间x(分钟)之间的函数关系的图象如图所示(A,B,C三点共线).王师傅说:“我开车通过隧道时,有一段连续2分钟恰好走了1.9千米”.你认为王师傅说有可能对吗?请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
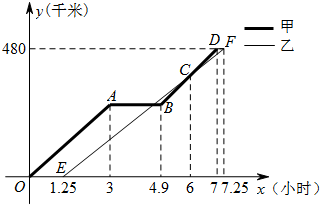 某市接到上级救灾的通知,派出甲、乙两个抗震救灾小组乘车沿同一路线赶赴距出发点480千米的灾区.乙组由于要携带一些救灾物资,比甲组迟出发1.25小时(从甲组出发时开始计时).图中的折线、线段分别表示甲、乙两组的所走路程y甲(千米)、y乙(千米)与时间x(小时)之间的函数关系对应的图象.请根据图象所提供的信息,解决下列问题:
某市接到上级救灾的通知,派出甲、乙两个抗震救灾小组乘车沿同一路线赶赴距出发点480千米的灾区.乙组由于要携带一些救灾物资,比甲组迟出发1.25小时(从甲组出发时开始计时).图中的折线、线段分别表示甲、乙两组的所走路程y甲(千米)、y乙(千米)与时间x(小时)之间的函数关系对应的图象.请根据图象所提供的信息,解决下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
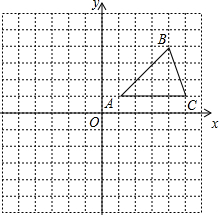 在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).
在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com