
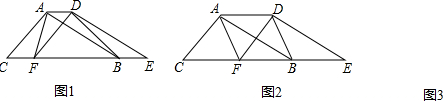
分析 (1)利用平行线的性质以及三角形面积关系得出答案;
(2)利用平行四边形的判定得出四边形AFBD为平行四边形,进而得出AF=$\frac{1}{2}$BC=BF,求出答案;
(3)根据题意画出图形,利用sin∠CGF=$\frac{CF}{CG}$求出即可.
解答 解:(1)S△ABC=S四边形AFBD,
理由:由题意可得:AD∥EC,
则S△ADF=S△ABD,
故S△ACF=S△ADF=S△ABD,
则S△ABC=S四边形AFBD;
(2)△ABC为等腰直角三角形,即:AB=AC,∠BAC=90°,
理由如下:∵F为BC的中点,
∴CF=BF,
∵CF=AD,
∴AD=BF,
又∵AD∥BF,
∴四边形AFBD为平行四边形,
∵AB=AC,F为BC的中点,
∴AF⊥BC,
∴平行四边形AFBD为矩形,
∵∠BAC=90°,F为BC的中点,
∴AF=$\frac{1}{2}$BC=BF,
∴四边形AFBD为正方形;
(3)如图3所示:
由(2)知,△ABC为等腰直角三角形,AF⊥BC,
设CF=k,则GF=EF=CB=2k,
由勾股定理得:CG=$\sqrt{5}$k,
sin∠CGF=$\frac{CF}{CG}$=$\frac{k}{\sqrt{5}k}$=$\frac{\sqrt{5}}{5}$.
点评 此题主要考查了正方形的判定以及等腰直角三角形的性质和锐角三角函数关系等知识,熟练应用正方形的判定方法是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
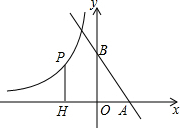 如图,直线y=-$\sqrt{3}$x+3分别与x轴、y轴交于A、B两点,点P是y=-$\frac{\sqrt{3}}{x}$(x<0)的图象上一点,PH⊥x轴于H,当以P为圆心,PH为半径的圆与直线AB相切时,OH的长为$\frac{\sqrt{15}-\sqrt{3}}{2}$.
如图,直线y=-$\sqrt{3}$x+3分别与x轴、y轴交于A、B两点,点P是y=-$\frac{\sqrt{3}}{x}$(x<0)的图象上一点,PH⊥x轴于H,当以P为圆心,PH为半径的圆与直线AB相切时,OH的长为$\frac{\sqrt{15}-\sqrt{3}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x(亩) | 20 | 25 | 30 | 35 |
| z(元) | 1700 | 1600 | 1500 | 1400 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
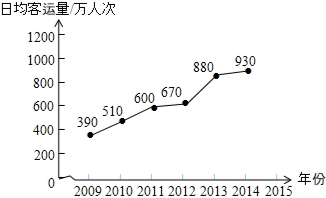 北京市2009-2014年轨道交通日均客运量统计如图所示.根据统计图中提供的信息,预估2015年北京市轨道交通日均客运量约980万人次,你的预估理由是因为2012-2013年发生数据突变,故参照2013-2014增长进行估算..
北京市2009-2014年轨道交通日均客运量统计如图所示.根据统计图中提供的信息,预估2015年北京市轨道交通日均客运量约980万人次,你的预估理由是因为2012-2013年发生数据突变,故参照2013-2014增长进行估算..查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 明天太阳从西方升起 | |
| B. | 掷一枚硬币,正面朝上 | |
| C. | 打开电视机,正在播放“河池新闻” | |
| D. | 任意-个三角形,它的内角和等于180° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com