
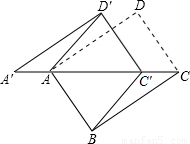
 (2009•咸宁)如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A′C′D′.
(2009•咸宁)如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A′C′D′. AC,AB=
AC,AB= AC,从而得到AB=BC′,所以四边形ABC′D′是菱形.
AC,从而得到AB=BC′,所以四边形ABC′D′是菱形. AC.
AC. AC.
AC.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源:2011年浙江省杭州市中考数学模拟试卷(24)(解析版) 题型:解答题
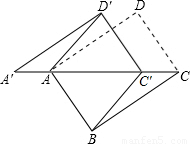 (2009•咸宁)如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A′C′D′.
(2009•咸宁)如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A′C′D′.查看答案和解析>>
科目:初中数学 来源:2010年初中数学第一轮复习教学案例.5.2.三角形的基本概念与基本性质(解析版) 题型:填空题
 ∠A;
∠A;
查看答案和解析>>
科目:初中数学 来源:2009年湖北省咸宁市中考数学试卷(解析版) 题型:解答题
 时,证明DC⊥OA;
时,证明DC⊥OA;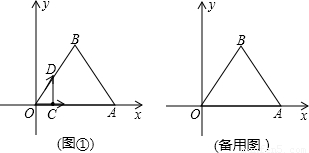
查看答案和解析>>
科目:初中数学 来源:2009年湖北省咸宁市中考数学试卷(解析版) 题型:填空题
 ∠A;
∠A;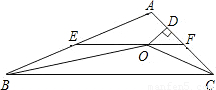
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com