
分析 设抛物线y=ax2+2ax+3与x轴的两交点坐标分别是(m,0),(n,0),则m、n是一元二次方程ax2+2ax+3=0的两个根,利用根与系数的关系得出m+n=-2,mn=$\frac{3}{a}$,根据抛物线y=ax2+2ax+3与x轴的两交点之间的距离为4,得出4-$\frac{12}{a}$=16,解方程即可.
解答 解:设抛物线y=ax2+2ax+3与x轴的两交点坐标分别是(m,0),(n,0),则m、n是一元二次方程ax2+2ax+3=0的两个根,
所以m+n=-2,mn=$\frac{3}{a}$.
∵抛物线y=ax2+2ax+3与x轴的两交点之间的距离为4,
∴(m-n)2=16,
∴(m+n)2=-4mn=16,
∴4-$\frac{12}{a}$=16,
∴a=-1.
故答案为-1.
点评 本题考查了抛物线与x轴的交点,二次函数与一元二次方程的关系,利用根与系数的关系以及完全平方公式列出关于a的方程是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | a3与b3 | B. | 3x2y与-4x2yz | C. | x2y与-xy2 | D. | -2a2b与$\frac{1}{2}$ba2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
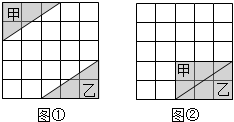 如图,在5×5的方格纸中,将如图①的三角形甲平移到如图②所示的位置,与三角形乙拼成一个长方形.正确的平移方法,可以先将甲向下平移3格,再向右平移2格得到.
如图,在5×5的方格纸中,将如图①的三角形甲平移到如图②所示的位置,与三角形乙拼成一个长方形.正确的平移方法,可以先将甲向下平移3格,再向右平移2格得到.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
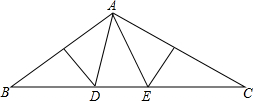 如图,△ABC的两边AB、AC的垂直平分线分别交边BC于点D、E,若△ABC的周长为26,AB+AC=14,则△ABE和△ACD的周长和是38.
如图,△ABC的两边AB、AC的垂直平分线分别交边BC于点D、E,若△ABC的周长为26,AB+AC=14,则△ABE和△ACD的周长和是38.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com