
已知:
 ,求
,求 的值.
的值.
科目:初中数学 来源: 题型:填空题
在△ABC中,P是AB上的动点(P异于A,B),过点P的一条直线截△ABC,使截得的三角形与△ABC相似,我们不妨称这种直线为过点P的△ABC的相似线.如图,∠A=36°,AB=AC,当点P在AC的垂直平分线上时,过点P的△ABC的相似线最多有 条.
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
如图是一张锐角三角形纸片,AD是BC边上的高,BC=40cm,AD=30cm,现从硬纸片上剪下一个长是宽2倍的周长最大的矩形,则所剪得的矩形周长为_____________cm.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知在△ABC中,AB=AC,BC比AB大3, ,点G是△ABC的重心,AG的延长线交边BC于点D.过点G的直线分别交边AB于点P、交射线AC于点Q.
,点G是△ABC的重心,AG的延长线交边BC于点D.过点G的直线分别交边AB于点P、交射线AC于点Q.
(1)求AG的长;
(2)当∠APQ=90º时,直线PG与边BC相交于点M.求 的值;
的值;
(3)当点Q在边AC上时,设BP= ,AQ=
,AQ= ,求
,求 关于
关于 的函数解析式,并写出它的定义域.[
的函数解析式,并写出它的定义域.[
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图1,梯形 中,
中, ∥
∥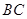 ,
, ,
, .一个动点
.一个动点 从点
从点 出发,以每秒
出发,以每秒 个单位长度的速度沿线段
个单位长度的速度沿线段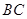 方向运动,过点
方向运动,过点 作
作 ,交折线段
,交折线段 于点
于点 ,以
,以 为边向右作正方形
为边向右作正方形 ,点
,点 在射线
在射线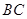 上,当
上,当 点到达
点到达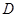 点时,运动结束.设点
点时,运动结束.设点 的运动时间为
的运动时间为 秒(
秒( ).
).
(1)当正方形 的边
的边 恰好经过点
恰好经过点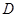 时,求运动时间
时,求运动时间 的值;
的值;
(2)在整个运动过程中,设正方形 与△
与△ 的重合部分面积为
的重合部分面积为 ,请直接写出
,请直接写出 与
与 之间的函数关系式和相应的自变量
之间的函数关系式和相应的自变量 的取值范围;
的取值范围;
(3)如图2,当点 在线段
在线段 上运动时,线段
上运动时,线段 与对角线
与对角线 交于点
交于点 ,将△
,将△ 沿
沿 翻折,得到△
翻折,得到△ ,连接
,连接 .是否存在这样的
.是否存在这样的 ,使△
,使△ 是等腰三角形?若存在,求出对应的
是等腰三角形?若存在,求出对应的 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如果一个图形经过分割,能成为若干个与自身相似的图形,我们称它为“相似分割的图形”,如图所示的等腰直角三角形和矩形就是能相似分割的图形.
(1)你能否再各举出一个 “能相似分割”的三角形和四边形?
(2)一般的三角形是否是“能相似分割的图形”?如果是请给出一种分割方案并画出图形,否则说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com