
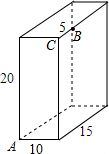
 如图,长方体的长为15cm,宽为10cm,高为20cm,点B到点C的距离5cm,一只蚂蚁如果沿着长方体的表面从A点爬到B点,需要爬行的最短距离是25.
如图,长方体的长为15cm,宽为10cm,高为20cm,点B到点C的距离5cm,一只蚂蚁如果沿着长方体的表面从A点爬到B点,需要爬行的最短距离是25. 分析 要求正方体中两点之间的最短路径,最直接的作法,就是将长方体展开,然后利用两点之间线段最短解答.
解答 解:如图:(1)AB=$\sqrt{B{D}^{2}+A{D}^{2}}$=$\sqrt{2{0}^{2}+1{5}^{2}}$=25;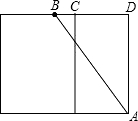
(2)AB=$\sqrt{A{E}^{2}+B{E}^{2}}$=$\sqrt{1{0}^{2}+2{5}^{2}}$=5 $\sqrt{29}$;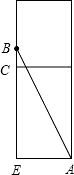
(3)AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{3{0}^{2}+{5}^{2}}$=5$\sqrt{37}$.
所以需要爬行的最短距离是25.
故答案为:25.
点评 本题考查了平面展开---最短路径问题,解题的关键是将图形展开,转化为直角三角形利用勾股定理解答.


科目:初中数学 来源: 题型:解答题
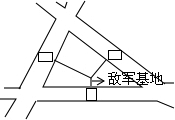 敌军基地在三条公路围成的三角区域内,我军一队战士在一条公路中点垂直射击,另一队战士在另一条公路中点垂直射击,均击中敌军基地,问第三队战士在公路何处垂直射击可击中目标?
敌军基地在三条公路围成的三角区域内,我军一队战士在一条公路中点垂直射击,另一队战士在另一条公路中点垂直射击,均击中敌军基地,问第三队战士在公路何处垂直射击可击中目标?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 有一块长为30m,宽为20m的矩形菜地,准备修筑同样宽的三条直路(如图),把菜地分成六块作为试验田,种植不同品种的蔬菜,并且种植蔬菜面积为矩形菜地面积的$\frac{3}{4}$,设道路的宽度为x m,下列方程:
有一块长为30m,宽为20m的矩形菜地,准备修筑同样宽的三条直路(如图),把菜地分成六块作为试验田,种植不同品种的蔬菜,并且种植蔬菜面积为矩形菜地面积的$\frac{3}{4}$,设道路的宽度为x m,下列方程:| A. | ①② | B. | ①③ | C. | ②③ | D. | ①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -3.5 | B. | +2.5  | C. | -0.6  | D. | +0.7  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com