
����Ŀ����ͼ��ʾ���ڵȱ�������ABC�У�BC��8cm������AG��BC����E�ӵ�A����������AG��1cm/s���ٶ��˶���ͬʱ��F�ӵ�B����������BC��2cm/s���ٶ��˶������˶�ʱ��Ϊt��s����
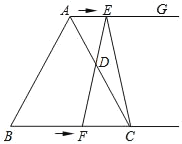
��1������EF����EF����AC�ߵ��е�Dʱ����֤���ı���AFCE��ƽ���ı��Σ�
��2����գ��ٵ�tΪ�� ��sʱ���ı���ACFE�����Σ��ڵ�tΪ�� ��sʱ����ACE������ǡ�ACF�������2����
���𰸡���1����������
��2����8����t=![]() ��y=
��y=![]() .
.
��������
��1���жϳ���ADE�ա�CDF�ó�AE��CF�����ɵó����ۣ�
��2���������AC��BC��8�������жϳ�AE��CF��AC��8�����ɵó����ۣ�
�����жϳ���ACE����ACF�ı�AE��CF�ϵĸ���ȣ������жϳ�AE��2CF���ٷ��������������������⼴�ɵó����ۣ�
�⣺��1����ͼ1��
��AG��BC��
���EAC=��FCA����AED=��CFD��
��EF����AC�ߵ��е�D��
��AD=CD��
���ADE�ա�CDF��AAS����
��AE=CF��
��AE��FC��
���ı���AFCE��ƽ���ı��Σ�
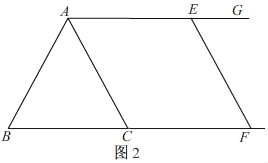
��2������ͼ2��
�ߡ�ABC�ǵȱ������Σ�
��AC=BC=8��
���ı���ACFE�����Σ�
��AE=CF=AC=BC=8���ҵ�F��BC�ӳ����ϣ����˶�֪��AE=t��BF=2t��
��CF=2t��8��t=8����t=8����CF=2t��8��
��CF=8=AC=AE���������⣬����t=8��ʱ���ı���ACFE�����Σ�
�ʴ�Ϊ��8��
����ƽ����AG��BC�ľ���Ϊh��
���ACE��AE�ϵĸ�Ϊh����ACF�ı�CF�ϵĸ�Ϊh��
�ߡ�ACE���������ACF�������2����
��AE=2CF������F���߶�BC��ʱ��0��t��4����CF=8��2t��AE=t��
��t=2��8��2t����
��![]()
����F��BC���ӳ�����ʱ��t��4����CF=2t��8��AE=t��
��t=2��2t��8����
��![]()
����t=![]() ���
���![]() ��ʱ����ACE���������ACF�������2����
��ʱ����ACE���������ACF�������2����
�ʴ�Ϊ��![]() ��
��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
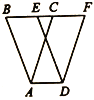
����Ŀ����ͼ���ڡ�ABC�У�![]() ������ABC��ÿ��2cm���ٶ���
������ABC��ÿ��2cm���ٶ���![]() ����ֱ������ƽ�ƣ�����ͼ�ζ�ӦΪ��DEF����ƽ��ʱ��Ϊt�룬��Ҫʹ
����ֱ������ƽ�ƣ�����ͼ�ζ�ӦΪ��DEF����ƽ��ʱ��Ϊt�룬��Ҫʹ![]() ��������
��������![]() ��ֵΪ_____�룮
��ֵΪ_____�룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣨x1��y1������x2��y2������x3��y3�����Ƿ���������y=��![]() ͼ���ϵĵ㣬����y1��0��y2��y3�������и�ʽ����ȷ���ǣ� ��
ͼ���ϵĵ㣬����y1��0��y2��y3�������и�ʽ����ȷ���ǣ� ��
A��x1��x2��x3 B��x1��x3��x2
C��x2��x1��x3 D��x2��x3��x1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ����֤��
����֤��![]() ���뽫֤��������д����.
���뽫֤��������д����.
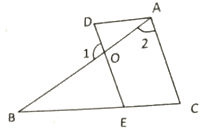
֤������![]() ����֪��
����֪��
�֡�![]() �� ��
�� ��
��________![]() ��
��
��![]() ____________�� ��
____________�� ��
��![]() ______________�� ��
______________�� ��
�֡�![]() ����֪��
����֪��
��![]() ________________��
________________��
��![]() �� ��
�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����̵�ƻ��ӳ��ҹ���![]() ���ֲ�ͬ�ͺŵĵ���ȣ�������8̨
���ֲ�ͬ�ͺŵĵ���ȣ�������8̨![]() �ͺ�20̨
�ͺ�20̨![]() �͵���ȣ����ʽ�7600Ԫ��������4̨
�͵���ȣ����ʽ�7600Ԫ��������4̨![]() �ͺ�15̨
�ͺ�15̨![]() �͵���ȣ����ʽ�5300Ԫ.
�͵���ȣ����ʽ�5300Ԫ.
��1����![]() �͵����ÿ̨�Ľ��۸��Ƕ���Ԫ��
�͵����ÿ̨�Ľ��۸��Ƕ���Ԫ��
��2�����̵꾭���ƻ��������ֵ���ȹ�50̨���������ڹ��������ֵ���ȵ��ʽ���12800Ԫ�������г����У�����һ̨![]() �͵���ȿɻ���80Ԫ������һ̨
�͵���ȿɻ���80Ԫ������һ̨![]() �͵���ȿɻ���120Ԫ.�����ֵ���������ʱ������õ���������5000Ԫ.�����ļ��ֽ������������ַ�����������������Ƕ��٣�
�͵���ȿɻ���120Ԫ.�����ֵ���������ʱ������õ���������5000Ԫ.�����ļ��ֽ������������ַ�����������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���ACB��90�㣬��ABC��25�㣬�Ե�CΪ��ת����˳ʱ����ת��õ���A��B��C���ҵ�A�ڱ�A��B���ϣ�����ת�ǵĶ���Ϊ��������

A. 65��B. 60��C. 50��D. 40��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AD����ABC�ĸ��ߣ���BC���Ͻ�ȡ��E��ʹ��CE��BD����E��EF��AB����C��CP��BC��EF�ڵ�P����B��BM��AC��M������EM��PM��
(1)�����ⲹȫͼ�Σ�
(2)��AD��DC��̽��EM��PM��������ϵ��λ�ù�ϵ��������֤����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
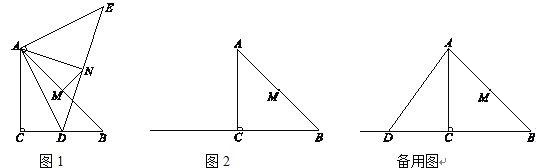
����Ŀ������ABC�У���ACB=90����AC=BC=4��MΪAB���е���D������BC��һ�����㣬����AD�����߶�AD�Ƶ�A��ʱ����ת90���õ��߶�AE������ED��NΪED���е㣬����AN��MN��
��1����ͼ1����BD=2ʱ��AN=___ __��NM��AB��λ�ù�ϵ��____ _____��
��2����4<BD<8ʱ��
�������ⲹȫͼ2��
���жϣ�1����NM��AB��λ�ù�ϵ�Ƿ����仯����֤����Ľ��ۣ�
��3������ME���ڵ�D�˶��Ĺ����У���BD�ij�Ϊ��ֵʱ��ME�ij���С����Сֵ�Ƕ��٣���ֱ��д�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У��Խ���AC��BD�ཻ�ڵ�O��BD��2AD��E��F��G�ֱ���OC��OD��AB���е㣬���н��ۣ��١�OBE��![]() ��ADO����EG��EF����GFƽ�֡�AGE����EF��GE��������ȷ����_____��
��ADO����EG��EF����GFƽ�֡�AGE����EF��GE��������ȷ����_____��

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com